(满分13分)某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米。
(1)若设休闲区的长 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于 的函数
的函数 的解析式;
的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
等比数列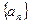 中,已知
中,已知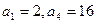 ,
,
(1)求数列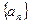 的通项公式
的通项公式
(2)若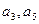 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 的通项公式及前n项和
的通项公式及前n项和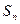
(本小题14分)
已知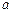 为实数,
为实数,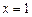 是函数
是函数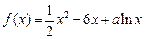 的一个极值点。
的一个极值点。
(Ⅰ)求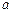 的值;
的值;
(Ⅱ)若函数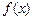 在区间
在区间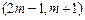 上单调递减,求实数
上单调递减,求实数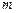 的取值范围;
的取值范围;
(Ⅲ)设函数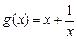 ,对于任意
,对于任意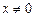 和
和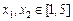 ,有不等式
,有不等式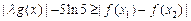 恒成立,求实数
恒成立,求实数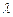 的取值范围
的取值范围
(本小题12分)
过椭圆
 的一个焦点
的一个焦点 且垂直于
且垂直于 轴的直线交椭圆于点
轴的直线交椭圆于点 。
。
(Ⅰ) 求椭圆C的方程;
求椭圆C的方程;
(Ⅱ)是否存在过点 的直线
的直线 与椭圆
与椭圆 交于两点
交于两点 、
、 ,使得
,使得 (其中
(其中 为弦
为弦 的中点)?若存在,求出直线
的中点)?若存在,求出直线 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
(本小题12分)
图甲是一个几何体的表面展开图,图乙是棱长为 的正方体。
的正方体。
(Ⅰ)若沿图甲中的虚线将四个三角形折叠起来,使点 、
、 、
、 、
、 重合,则可以围成怎样的几何体?请求出此几何体的体积;
重合,则可以围成怎样的几何体?请求出此几何体的体积;
(Ⅱ)需要多少个(I)的几何体才能拼成一个图乙中的正方 体?请按图乙中所标字母写出这几个几何体的名称;
体?请按图乙中所标字母写出这几个几何体的名称;
(Ⅲ)在图乙中,点 为棱
为棱 上的动点,试判断
上的动点,试判断 与平面
与平面 是否垂直,并说明理由。
是否垂直,并说明理由。

(本小题12分)
在某次高三质检考试后,抽取了九位同学的数学成绩进行统计,下表是九位同学的选择题和填空题的得分情况:
| 选择题 |
40 |
55 |
50 |
45 |
50 |
40 |
45 |
60 |
40 |
| 填空题 |
12 |
16 |
  |
12 |
16 |
12 |
8 |
12 |
8 |
(Ⅰ)若这九位同学填空题得分的平均分为 ,试求表中
,试求表中 的值及他们填空题得分的标准差;
的值及他们填空题得分的标准差;
(Ⅱ)在(Ⅰ)的条件下,记这九位同学的选择题得分组成的集合为 ,填空题得分组成的集合为
,填空题得分组成的集合为 .若同学甲的解答题的得分是
.若同学甲的解答题的得分是 ,现分别从集合
,现分别从集合 、
、 中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于
中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于 分的概率
分的概率