由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,
小数点后的一位数字为叶)如图示:
| |
|
| 4 |
3 5 6 6 6 7 7 7 8 8 9 9 |
| 5 |
0 1 1 2 |
(1)指出这组数据的众数和中位数;
(2)若视力测试结果不低于5.0,则称为“健康视力”,求校医从这16人中随机选取3人,至多有1人是“健康视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记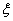 表示抽到“健康视力”学生的人数,求
表示抽到“健康视力”学生的人数,求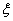 的分布列及数学期望
的分布列及数学期望
设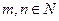 ,
,
 .
.
(1)当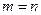 =2011时,记
=2011时,记 ,
,
求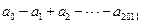 ;
;
(2)若 展开式中
展开式中 的系数是20,则当
的系数是20,则当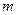 、
、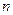 变化时,试求
变化时,试求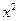 系数的最小值.
系数的最小值.
已知在一个二阶矩阵M的变换作用下, 点 变成了点
变成了点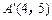 ,点
,点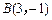 变成了点
变成了点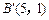 ,求矩阵M.
,求矩阵M.
已知数列a,b,c为各项都是正数的等差数列,公差为d(d>0),在a,b之间和b,c之间共插入m个实数后,所得到的m+3个数所组成的数列{an}是等比数列,其公比为q.
(1)若a=1,m=1,求公差d ;
;
(2)若在a,b之间和b,c之间所插入数的个数均为奇数,求所插入的m数的乘积(用a,c,m表示)
(3)求证:q是无理数.
已知f (x)=ax-ln(-x),x∈(-e,0),g(x)=-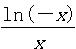 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R.
(1)讨论a=-1时, f ( x)的单调性、极值;
x)的单调性、极值;
(2)求证:在(1)的条件下,|f (x)|>g(x)+1/2;
(3)是否存在实数a,使f (x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由.
已知椭圆C: +y2=1,过点(m,0)作圆x2+y2=1的切线l交椭圆G于A、B两点.
+y2=1,过点(m,0)作圆x2+y2=1的切线l交椭圆G于A、B两点.
(1)求椭圆C的焦点坐标和离心率;
(2)将|AB|表示为m的函数,并求|AB|的最大值