如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.
(1)证明:EM⊥BF;
(2)求平面 BEF 与平面ABC 所成的二面角的余弦值.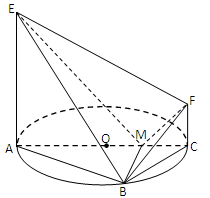
.如图:四边形 为正方形,
为正方形, 为矩形,
为矩形, 平面
平面 ,
, 为
为 的中点(Ⅰ)求证
的中点(Ⅰ)求证 平面
平面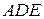 ;(Ⅱ)求证平面
;(Ⅱ)求证平面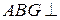 平面
平面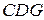 ;
;
(Ⅲ)求二面角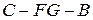 的余弦植。
的余弦植。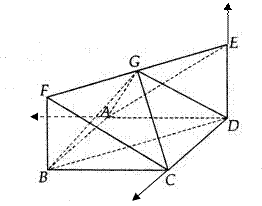
(本小题满分13分)在一个盒子中,放有标号分别为 ,
, ,
, 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点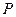 的坐标为
的坐标为 ,记
,记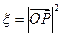
(Ⅰ) 求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率
取得最大值”的概率
(Ⅱ) 求随机变量 的分布列和数学期望
的分布列和数学期望
(本小题满分13分) 已知函数
已知函数
(Ⅰ)(设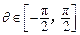 ,且
,且 ,求
,求 的值
的值
(Ⅱ)在△ABC中,AB=1, ,且△ABC的面积为
,且△ABC的面积为 ,求sinA+sinB的值
,求sinA+sinB的值
(本小题满分12分)
已知点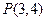 是椭圆
是椭圆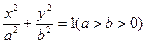 上
上 一点,离心率
一点,离心率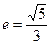 ,
,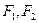 是椭圆的两
是椭圆的两
个焦点.
(1)求椭圆的面积;
(2)求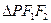 的面积。
的面积。
(本小题满分12分)
已知复数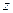 满足:
满足: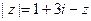 ,求
,求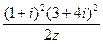 的值.
的值.