(本题满分15分)
已知椭圆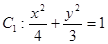 ,抛物线
,抛物线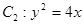 ,过椭圆
,过椭圆 右顶点的直线
右顶点的直线 交抛物线
交抛物线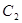 于
于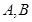 两点,射线
两点,射线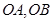 分别与椭圆交于点
分别与椭圆交于点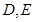 ,点
,点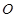 为原点.
为原点.
(Ⅰ)求证:点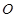 在以
在以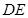 为直径的圆的内部;
为直径的圆的内部;
(Ⅱ)记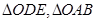 的面积分别为
的面积分别为 ,问是否存在直线
,问是否存在直线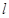 使
使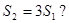 若存在,求出直线
若存在,求出直线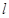 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.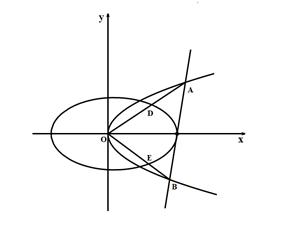
附加题: 对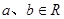 ,记
,记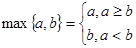 ,函数
,函数 .
.
(1)作出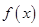 的图像,并写出
的图像,并写出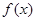 的解析式;
的解析式;
(2)若函数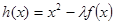 在
在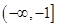 上是单调函数,求
上是单调函数,求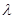 的的取值范围.
的的取值范围.
已知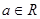 ,函数
,函数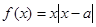 ,
,
(1)当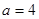 时,写出函数
时,写出函数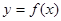 的单调递增区间;
的单调递增区间;
(2)当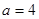 时,求
时,求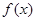 在区间
在区间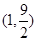 上最值;
上最值;
(3)设 ,函数
,函数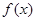 在
在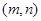 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出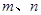 的取值范围(用
的取值范围(用 表示)
表示)
已知二次函数 的最小值为1,且
的最小值为1,且
(1)求 的解析式;
的解析式;
(2)若 在区间
在区间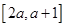 上是单调函数,求实数
上是单调函数,求实数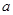 的取值范围.
的取值范围.
设函数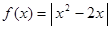
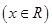 .
.
(1)先完成下列表格,再画出函数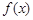 在区间
在区间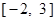 上的图像;
上的图像;
(2)根据图像写出该函数在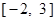 上的单调区间;
上的单调区间;
(3)根据图像写出该函数在区间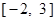 上的值域.
上的值域.
| x |
…… |
-2 |
0 |
1 |
2 |
3 |
…… |
| y |
已知定义域为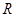 的奇函数
的奇函数 ,当
,当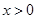 时,
时,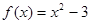 .
.
(1)当 时,求函数
时,求函数 的解析式;
的解析式;
(2)求函数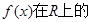 解析式;
解析式;
(3)解方程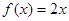 .
.