(本小题满分14分)已知函数 ,
,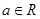
(1) 若函数 在
在 上是减函数,求实数
上是减函数,求实数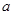 的取值范围;
的取值范围;
(2) 令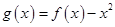 ,是否存在实数
,是否存在实数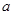 ,当
,当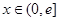 (
(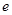 是自然常数)时,函数
是自然常数)时,函数 的最小值是
的最小值是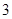 ,若存在,求出
,若存在,求出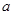 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)求证:当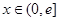 时,
时,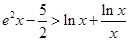
已知
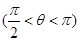 .
.
(1)求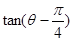 的值;
的值;
(2)求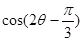 的值.
的值.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.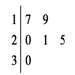
(1)若日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?
(2)从这6名工人中任取2人,设这两人加工零件的个数分别为 ,求
,求 的概率.
的概率.
已知数列{an}是等差数列,数列{bn}是等比数列,且对任意的n∈N*,都有a1b1+a2b2+a3b3+···+anbn=n·2n+3.
(1)若{bn}的首项为4,公比为2,求数列{an+bn}的前n项和Sn;
(2)若a1=8.
①求数列{an}与{bn}的通项公式;
②试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它r(r∈N,r≥2)项的和?若存在,请求出该项;若不存在,请说明理由.
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别写出用x表示y和S的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?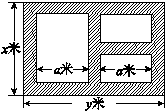
已知{an}是公比为q的等比数列,且am、am+2、am+1成等差数列.
(1)求q的值;
(2)设数列{an}的前n项和为Sn,试判断Sm、Sm+2、Sm+1是否成等差数列?并说明理由.