从4名男生,3名女生中选出三名代表:
(1)不同的选法共有多少种?
(2)至少有一名女生的不同的选法共有多少种?
(3)代表中男、女生都要有的不同的选法共有多少种?
如图,现要在边长为 的正方形
的正方形 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为
内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为 (
(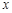 不小于
不小于 )的扇形花坛,以正方形的中心为圆心建一个半径为
)的扇形花坛,以正方形的中心为圆心建一个半径为 的圆形草地.为了保证道路畅通,岛口宽不小于
的圆形草地.为了保证道路畅通,岛口宽不小于 ,绕岛行驶的路宽均不小于
,绕岛行驶的路宽均不小于 .
.
(1)求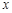 的取值范围;(运算中
的取值范围;(运算中 取
取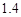 )
)
(2)若中间草地的造价为 元
元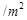 ,四个花坛的造价为
,四个花坛的造价为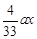 元
元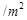 ,其余区域的造价为
,其余区域的造价为 元
元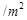 ,当
,当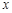 取何值时,可使“环岛”的整体造价最低?
取何值时,可使“环岛”的整体造价最低?
如图,在正三棱柱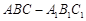 中,
中, ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面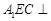 平面
平面 .
.
在 中,角
中,角 ,
,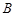 ,
, 所对的边分别是
所对的边分别是 ,
, ,
,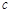 ,已知
,已知 ,
,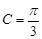 .
.
(1)若 的面积等于
的面积等于 ,求
,求 ,
, ;
;
(2)若 ,求
,求 的面积.
的面积.
已知函数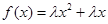 ,
, ,
,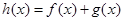 ,其中
,其中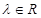 ,且
,且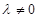 .
.
⑴当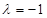 时,求函数
时,求函数 的最大值;
的最大值;
⑵求函数 的单调区间;
的单调区间;
⑶设函数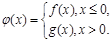 若对任意给定的非零实数
若对任意给定的非零实数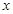 ,存在非零实数
,存在非零实数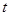 (
( ),使得
),使得 成立,求实数
成立,求实数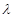 的取值范围.
的取值范围.
已知函数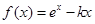 .
.
(Ⅰ)若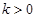 ,且对于任意
,且对于任意 恒成立,试确定实数
恒成立,试确定实数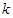 的取值范围;
的取值范围;
(Ⅱ)设函数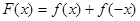 ,
,
求证: