已知函数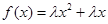 ,
, ,
,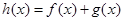 ,其中
,其中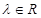 ,且
,且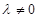 .
.
⑴当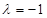 时,求函数
时,求函数 的最大值;
的最大值;
⑵求函数 的单调区间;
的单调区间;
⑶设函数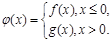 若对任意给定的非零实数
若对任意给定的非零实数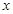 ,存在非零实数
,存在非零实数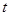 (
( ),使得
),使得 成立,求实数
成立,求实数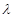 的取值范围.
的取值范围.
(本小题满分12分)
已知直线l1:4x:-3y+6=0和直线l2x=-p/2:.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(I )求抛物线C的方程;
(II)若以拋物线上任意一点M为切点的直线l与直线l2交于点N,试问在x轴上是否存 在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标,若不存在,请说明理由.
(本小题满分12分)
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1丄底面ABC.
(I)若M、N分别是AB,A1C的中点,求证:MN//平面BCC1B1
(II)若三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面 ABC所成的角为60°.问在线段A1C1上是否存在一点P,使得平面B1CP丄平面ACC1A1,若存在,求C1P与PA1的比值,若不存在,说明 理由.
(本小题满分12分)
某市的教育研究机构对全市高三学生进行综合素质 测试,随机抽取了部分学生的成绩,得到如图所示的成绩 频率分布直方图.
(I )估计全市学生综合素质成绩的平均值;
(II)若评定成绩不低于8o分为优秀.视频率为概率,从 全市学生中任选3名学生(看作有放回的抽样),变量 表示 3名学生中成绩优秀的人数,求变量
表示 3名学生中成绩优秀的人数,求变量 的分布列及期望
的分布列及期望 )
)
(本小题满分12分)
已知函数
(I)求函数f(x)的最小正周期;
(II)求函数f(x)在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)
已知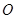 为坐标原点,点
为坐标原点,点 分别在
分别在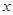 轴
轴 轴上运动,且
轴上运动,且 =8,动点
=8,动点 满足
满足 =
=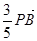 ,设点
,设点 的轨迹为曲线
的轨迹为曲线 ,定点为
,定点为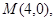 直线
直线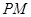 交曲线
交曲线 于另外一点
于另外一点
(1)求曲线 的方程;
的方程;
(2)求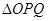 面积的最大值。
面积的最大值。