(本小题满分12分)
已知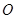 为坐标原点,点
为坐标原点,点 分别在
分别在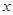 轴
轴 轴上运动,且
轴上运动,且 =8,动点
=8,动点 满足
满足 =
=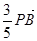 ,设点
,设点 的轨迹为曲线
的轨迹为曲线 ,定点为
,定点为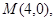 直线
直线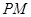 交曲线
交曲线 于另外一点
于另外一点
(1)求曲线 的方程;
的方程;
(2)求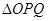 面积的最大值。
面积的最大值。
已知向量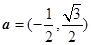 ,
, ,
,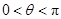 .
.
(1)若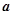 ∥
∥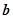 ,求角
,求角 的大小;
的大小;
(2)若 ,求
,求 的值.
的值.
(本小题满分14分)已知函数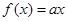 ,
,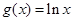 ,其中
,其中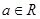 .
.
(1)若函数 ,当
,当 时,求函数
时,求函数 的极值;
的极值;
(2)若函数 在区间
在区间 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;
(3)证明: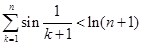 .
.
(本小题满分14分)已知抛物线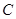 :
: 的焦点为
的焦点为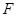 ,点
,点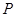 是直线
是直线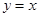 与抛物
与抛物
线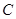 在第一象限的交点,且
在第一象限的交点,且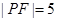 .
.
(1)求抛物线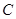 的方程;
的方程;
(2)设直线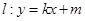 与抛物线
与抛物线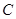 有唯一公共点
有唯一公共点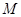 ,且直线
,且直线 与抛物线的准线交于点
与抛物线的准线交于点 ,试探究,在
,试探究,在
坐标平面内是否存在点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求出点
?若存在,求出点 的坐标,若不存在,
的坐标,若不存在,
说明理由.
(本小题满分14分)已知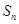 为数列
为数列 的前
的前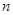 项和,
项和,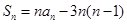 (
( ),且
),且 .
.
(1)求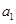 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)求证: .
.
(本小题满分14分)如图,已知 中,
中, ,
, ,
, ⊥
⊥
平面 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)设平面
 平面
平面 ,求证
,求证 ;
;
(3)求四棱锥B-CDFE的体积V.