如图,四面体 中,
中,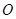 、
、 分别是
分别是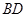 、
、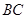 的中点,
的中点,
(1)求证: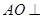 平面
平面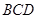 ;
;
(2)求直线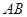 与平面
与平面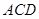 所成角的余弦值;
所成角的余弦值;
(3)求点 到平面
到平面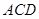 的距离。
的距离。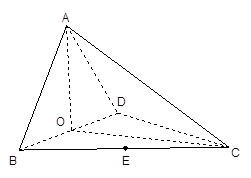
经过长期的观测得到:在交通繁忙的时段内,蚌埠市解放路某路段汽车的车流量 (千辆/h)与汽车的平均速度
(千辆/h)与汽车的平均速度 (
( )之间的函数关系为
)之间的函数关系为 。
。
(1)在该时段内,当汽车的平均速度 为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
(2)若要求在该时段内车流量超过10千辆/h,则汽车的平均速度应在什么范围内?
蚌埠市某中学高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
(1)求x和y的值;
(2)计算甲组7位学生成绩的方差 ;
;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲组至少有一名学生的概率.
已知 是公比为
是公比为 的等比数列,且
的等比数列,且 成等差数列。
成等差数列。
(1)求 的值;
的值;
(2)设 是以
是以 为首项,
为首项, 为公差的等差数列,求
为公差的等差数列,求 的前
的前 项和
项和 。
。
已知等差数列 的公差为
的公差为 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前
的前 学科王项和为
学科王项和为 ,求证:
,求证: .
.
某家居装饰设计的形状是如图所示的直三棱柱 ,其中,
,其中, ,
, 是边长为2(单位:米)的正方形,
是边长为2(单位:米)的正方形, ,点
,点 为棱
为棱 上的动点.
上的动点.
(Ⅰ)现需要对该装饰品的表面进行涂漆处理,假设每平方米的油漆费是40元,则需油漆费多少元?(提示: ,结果保留到整数位)
,结果保留到整数位)
(Ⅱ)当点 为何位置时,
为何位置时, 平面
平面 ?
?