对某班级50名同学一年来参加社会实践的次数进行的调查统计，得-优题课

题文

对某班级50名同学一年来参加社会实践的次数进行的调查统计，得到如下频率分布表：

参加次数	0	1	2	3
人数	0.1	0．2	0.4	0.3

根据上表信息解答以下问题：
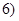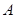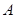(1)从该班级任选两名同学，用η表示这两人参加社会实践次数之和，记“函数在区间，内有零点”的事件为，求发生的概率；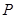
(2)从该班级任选两名同学，用ξ表示这两人参加社会实践次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ

科目数学题型解答题难度较易

知识点：随机思想的发展

登录免费查看答案和解析

相关试题

已知抛物线 $C : y^{2} = 2 p x (p > 0)$ 的焦点为 $F$ ，直线 $y = 4$ 与 $y$ 轴的交点为 $P$ ，与 $C$ 的交点为 $Q$ ，且 $|Q F| = \frac{5}{4} |P Q|$ .
(1)求抛物线 $C$ 的方程；
(2)过F的直线 $l$ 与 $C$ 相交于 $A, B$ 两点，若 $A B$ 的垂直平分线 $l `$ 与 $C$ 相交于 $M, N$ 两点，且 $A, M, B, N$ 四点在同一个圆上，求直线 $l$ 的方程.

函数 $f (x) = a x^{3} + 3 x^{2} + 3 x (a \neq 0)$ .
（1）讨论函数 $f (x)$ 的单调性；
（2）若函数 $f (x)$ 在区间（1，2）是增函数,求 $a$ 的取值范围.

设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6，0.5,0.5,0.4，各人是否使用设备相互独立，
（1）求同一工作日至少3人需使用设备的概率；
(2)实验室计划购买 $k$ 台设备供甲、乙、丙、丁使用，若要求"同一工作日需使用设备的人数大于 $k$ 的概率小于0.1，求 $k$ 的最小值.

如图，三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，点 $A_{1}$ 在平面 $A B C$ 内的射影 $D$ 在 $A C$ 上， $∠ A C B = 90 °$ ， $B C = 1$ ， $A C = C C_{1} = 2$

(1)证明： $A C_{1} ⊥ A_{1} B$

(2)设直线 $A A_{1}$ 与平面 $B C C_{1} B_{1}$ 的距离为 $\sqrt{3}$ ，求二面角 $A_{1} - A B - C$ 的大小.

$△ A B C$ 的内角 $A, B, C$ 的对边分别是 $a, b, c$ ，已知 $3 a \cos C = 2 \cos A, \tan A = \frac{1}{3}$ ,求 $B$ .

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号