某高中采取分层抽样的方法从应届高二学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
| 性别 科目 |
男 |
女 |
| 文科 |
2 |
5 |
| 理科 |
10 |
3 |
(Ⅰ)若在该样本中从报考文科的男生和报考理科的女生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用独立性检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关? (参考公式和数据:χ2 (其中
(其中 ))
))
设命题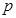 :关于x的函数
:关于x的函数 为增函数;命题
为增函数;命题 :不等式
:不等式 对一切正实数均成立. (1)若命题
对一切正实数均成立. (1)若命题 为真命题,求实数
为真命题,求实数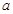 的取值范围;
的取值范围;
(2)命题“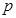 或
或 ”为真命题,且“
”为真命题,且“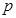 且
且 ”为假命题,求实数
”为假命题,求实数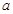 的取值范围.
的取值范围.
若点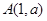 在直线
在直线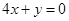 上,求经过点
上,求经过点 ,且与直线
,且与直线 平行的直线的方程。
平行的直线的方程。
如右图,在平面直角坐标系 中,已知“葫芦”曲线
中,已知“葫芦”曲线 由圆弧
由圆弧 与圆弧
与圆弧 相接而成,两相接点
相接而成,两相接点 均在直线
均在直线 上.圆弧
上.圆弧 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点 ,半径为
,半径为 ;圆弧
;圆弧 过点
过点 .
.
(I)求圆弧 的方程;
的方程;
(II)已知直线 :
: 与“葫芦”曲线
与“葫芦”曲线 交于
交于 两点.当
两点.当 时,求直线
时,求直线 的方程.
的方程.
设过点 的直线与椭圆
的直线与椭圆 相交于A,B两个不同的点,且
相交于A,B两个不同的点,且 .记O为坐标原点.求
.记O为坐标原点.求 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
如图,几何体 中,四边形
中,四边形 为平行四边形,且面
为平行四边形,且面
 面
面 ,
, ,且
,且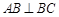 ,
,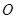 为
为 中点.
中点.
(Ⅰ)证明: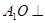 平面
平面 ;
;
(Ⅱ)求直线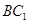 与底面
与底面 所成角的正弦值.
所成角的正弦值.