（本小题满分12分）如图，在四棱锥P-ABCD的底面是边长为2的正方形，
PD⊥平面ABCD，E、F分别是PB、AD的中点，PD=2．
（1）求证：BC⊥PC；
（2）求证：EF//平面PDC；
（3）求三棱锥B—AEF的体积。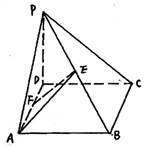
（本大题满分18分）本大题共有3个小题，第1小题满分4分，第2小题满6分，第3小题满8分.
已知函数
；
，
（1）当
为偶函数时，求
的值。
（2）当
时，
在
上是单调递增函数，求
的取值范围。
（3）当
时，（其中
，
），若
，且函数
的图像关于点
对称，在
处取得最小值，试探讨
应该满足的条件。
（本大题满分18分）本大题共有3个小题，第1小题满分4分，第2小题满6分，第3小题满8分.
已知集合
具有性质
：对任意
，
与
至少一个属于
.
（1）分别判断集合
与
是否具有性质，并说明理由；
（2）①求证：
；
②求证：
；
（3）研究当
和
时，集合中的数列
是否一定成等差数列.
（本大题满分14分）
已知中心在原点，顶点A1、A2在x轴上，其渐近线方程是
，双曲线过点
(1)求双曲线方程
(2)动直线
经过
的重心G，与双曲线交于不同的两点M、N，问:是否存在直线,使G平分线段MN，证明你的结论
本题共有2个小题，第1小题满分4分，第2小题满分8分.
已知
，函数
.
(Ⅰ)当
时，求使
成立的
的集合；
(Ⅱ)求函数
在区间
上的最小值.
（本题满分12分，每一问6分）
如图，弧
是半径为
的半圆，
为直径，点
为弧的中点，点
和点
为线段
的三等分点，线段
与弧
交于点
，且
，平面外一点
满足
平面
,
。
⑴证明：
；
⑵ 将
（及其内部）绕所在直线旋转一周形成一几何体，求该几何体的体积。