(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知函数 ;
;
 ,
,
(1)当 为偶函数时,求
为偶函数时,求 的值。
的值。
(2)当 时,
时, 在
在 上是单调递增函数,求
上是单调递增函数,求 的取值范围。
的取值范围。
(3)当 时,(其中
时,(其中 ,
, ),若
),若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。
已知函数
(Ⅰ)求函数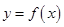 的单调区间;
的单调区间;
(Ⅱ)若函数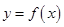 在
在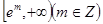 上有零点,求
上有零点,求 的最大值.
的最大值.
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中,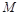 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.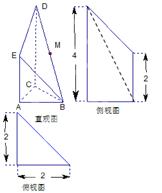
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
已知 中,
中,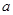 、
、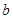 、
、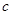 是三个内角
是三个内角 、
、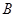 、
、 的对边,关于
的对边,关于 的不等式
的不等式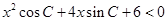
的解集是空集.
(Ⅰ)求角 的最大值;
的最大值;
(Ⅱ)若 ,
, 的面积
的面积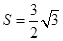 ,求当角
,求当角 取最大值时
取最大值时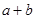 的值.
的值.
如图,在三棱锥 中,侧面
中,侧面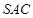 与底面
与底面 垂直,
垂直, 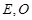 分别是
分别是 的中点,
的中点, ,
,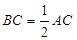 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若点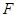 为线段
为线段 的中点,求异面直线
的中点,求异面直线 与
与 所成角的正切值.
所成角的正切值.
已知向量
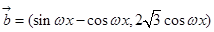 ,设函数
,设函数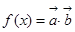
 的图象关于直线
的图象关于直线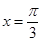 对称,其中常数
对称,其中常数

(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)将函数 的图像向左平移
的图像向左平移 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 在区间
在区间 的图像.
的图像.