(本小题满分12分)
2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K
和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员
的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前
训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
| 动作 |
K |
D |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
 |
 |
 |
 |
乙系列:
| 动作 |
K |
D |
||
| 得分 |
90 |
50 |
20 |
0 |
| 概率 |
 |
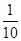 |
 |
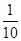 |
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(1)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(2)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX.
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如右表:
| 性别 是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中,需要志愿者提供帮助的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中需要志愿者提供帮助的老年人比例?说明理由。
附: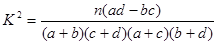
 |
0.050 |
0.010 |
0.001 |
| 3.841 |
6.635 |
10.828 |
已知: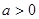 ,求证:
,求证: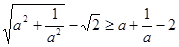
已知: 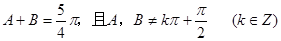
求证:
计算:(1) 
(2)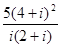
实数m取什么值时,复数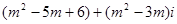 是
是
(1)实数;(2)虚数;(3)纯虚数。