设函数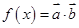 ,其中
,其中
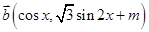
(1)求函数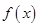 的最小正周期和在
的最小正周期和在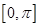 上的单调递增区间;
上的单调递增区间;
(2)当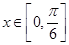 时,
时,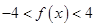 恒成立,求实数
恒成立,求实数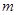 的取值范围.
的取值范围.
已知 ,求
,求 的值
的值
设 是定义在
是定义在 上的函数,若对任何实数
上的函数,若对任何实数 以及
以及 中的任意两数
中的任意两数 、
、 ,恒有
,恒有 ,则称
,则称 为定义在
为定义在 上的
上的 函数.
函数.
(1)证明函数 是定义域上的
是定义域上的 函数;
函数;
(2)判断函数 是否为定义域上的
是否为定义域上的 函数,请说明理由;
函数,请说明理由;
(3)若 是定义域为
是定义域为 的函数,且最小正周期为
的函数,且最小正周期为 ,试证明
,试证明 不是
不是 上的
上的 函数.
函数.
对于正项数列 ,若
,若 对一切
对一切 恒成立,则
恒成立,则 对
对 也恒成立是真命题.
也恒成立是真命题.
(1)若 ,
, ,且
,且 ,求证:数列
,求证:数列 前
前 项和
项和 ;
;
(2)若 ,
, ,求证:
,求证: .
.
曲线 是平面内到直线
是平面内到直线 和直线
和直线 的距离之积等于常数
的距离之积等于常数 的点的轨迹,设曲线
的点的轨迹,设曲线 的轨迹方程
的轨迹方程 .
.
(1)求曲线 的方程
的方程 ;
;
(2)定义:若存在圆 使得曲线
使得曲线 上的每一点都落在圆
上的每一点都落在圆 外或圆
外或圆 上,则称圆
上,则称圆 为曲线
为曲线 的收敛圆.判断曲线
的收敛圆.判断曲线 是否存在收敛圆?若存在,求出收敛圆方程;若不存在,请说明理由.
是否存在收敛圆?若存在,求出收敛圆方程;若不存在,请说明理由.
为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车 辆,混合动力型公交车
辆,混合动力型公交车 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加 ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入 辆.设
辆.设 、
、 分别为第
分别为第 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设 、
、 分别为
分别为 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
(1)求 、
、 ,并求
,并求 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数 ;
;
(2)该市计划用 年的时间完成全部更换,求
年的时间完成全部更换,求 的最小值.
的最小值.