(本小题共14分)如图,在四棱锥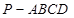 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为 的中点,
的中点, .
.
(Ⅰ)求证:
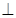 平面
平面 ;
;
(Ⅱ)点 在线段
在线段 上,
上, ,试确定
,试确定 的值,使
的值,使 平面
平面 ;
;
(Ⅲ)若 平面
平面 ,平面
,平面 平面
平面 ,求二面角
,求二面角 的大小.
的大小.
右图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
,
 ,且
,且 ,(1)求证:BE//平面PDA;
,(1)求证:BE//平面PDA;
(2)若N为线段 的中点,求证:
的中点,求证: 平面
平面 ;
;
(3)若 ,求平面PBE与平面ABCD所成的二面角的大小.
,求平面PBE与平面ABCD所成的二面角的大小.
已知复数 ,
, ,且
,且 .(1)若
.(1)若 且
且
 ,求
,求 的值;(2)设
的值;(2)设 =
= ,已知当
,已知当 时,
时,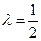 ,试求
,试求 的值.
的值.
已知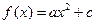 的图象经过点
的图象经过点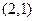 ,且在
,且在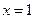 处的切线方程是
处的切线方程是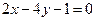
(1)求 的解析式;
的解析式;
(2)点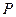 是直线
是直线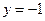 上的动点,自点
上的动点,自点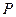 作函数
作函数 的图象的两条切线
的图象的两条切线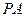 、
、 (点
(点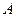 、
、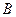 为切点),求证直线
为切点),求证直线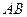 经过一个定点,并求出定点的坐标。
经过一个定点,并求出定点的坐标。
已知函数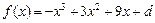 。
。
(1)求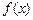 的单调区间;
的单调区间;
(2)如果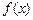 在区间
在区间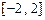 上的最小值为
上的最小值为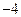 ,求实数
,求实数 以及在该区间上的最大值.
以及在该区间上的最大值.
已知两定点 ,动点
,动点 满足
满足 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)设点 的轨迹为曲线
的轨迹为曲线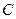 ,试求出双曲线
,试求出双曲线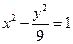 的渐近线与曲线
的渐近线与曲线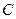 的交点坐标。
的交点坐标。