(本小题满分12分)在锐角 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 .
.
(I)求角 的大小;
的大小;
(Ⅱ)设 ,试
,试 求的取值范围.
求的取值范围.
(本小题满分14分)某农场计划种植甲、乙两个品种的蔬菜,总面积不超过 亩,总成本不超过
亩,总成本不超过 万元.甲、乙两种蔬菜的成本分别是每亩
万元.甲、乙两种蔬菜的成本分别是每亩 元和每亩
元和每亩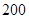 元.假设种植这两个品种的蔬菜,能为该农场带来的收益分别为每亩
元.假设种植这两个品种的蔬菜,能为该农场带来的收益分别为每亩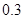 万元和每亩
万元和每亩 万元.问该农场如何分配甲、乙两种蔬菜的种植面积,可使农场的总收益最大,最大收益是多少万元?
万元.问该农场如何分配甲、乙两种蔬菜的种植面积,可使农场的总收益最大,最大收益是多少万元?
(本小题满分12分)设命题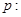 实数
实数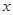 满足
满足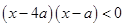 ,其中
,其中 ,命题
,命题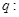 实数
实数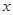 满足
满足 .
.
(1)若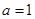 ,且
,且 为真,求实数
为真,求实数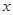 的取值范围;
的取值范围;
(2)若 是
是 成立的必要不充分条件,求实数
成立的必要不充分条件,求实数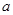 的取值范围.
的取值范围.
(本小题满分12分)在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, 且
且 .
.
(1)求 的面积;
的面积;
(2)若 ,求角
,求角 .
.
已知 ,
, 为圆
为圆 :
: 与
与 轴的交点(A在B上),过点
轴的交点(A在B上),过点 的直线
的直线 交圆
交圆 于
于 两点.
两点.
(1)若弦 的长等于
的长等于 ,求直线
,求直线 的方程;
的方程;
(2)若 都不与
都不与 ,
, 重合时,是否存在定直线
重合时,是否存在定直线 ,使得直线
,使得直线 与
与 的交点恒在直线
的交点恒在直线 上.若存在,求出直线
上.若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
如图,甲、乙两个企业的用电负荷量 关于投产持续时间
关于投产持续时间 (单位:小时)的关系
(单位:小时)的关系 均近似地满足函数
均近似地满足函数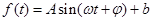
 .
.
(1)根据图象,求函数 的解析式;
的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过 ,现采用错峰用电的方式,让企业乙比企业甲推迟
,现采用错峰用电的方式,让企业乙比企业甲推迟
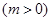 小时投产,求
小时投产,求 的最小值.
的最小值.