.(本小题满分14分)
设函数 (
(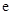 为自然对数的底数),
为自然对数的底数),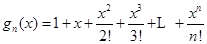 (
(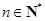 ).
).
(1)证明:
 ;
;
(2)当 时,比较
时,比较 与
与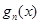 的大小,并说明理由;
的大小,并说明理由;
(3)证明: (
(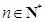 ).
).
(本小题共13分)将 这
这 个数随机排成一列,得到的一列数
个数随机排成一列,得到的一列数 称为
称为 的一个排列.定义
的一个排列.定义
 为排列
为排列 的波动强度.
的波动强度.
(Ⅰ)当 时,写出排列
时,写出排列 的所有可能情况及所对应的波动强度;
的所有可能情况及所对应的波动强度;
(Ⅱ)当 时,求
时,求 的最大值,并指出所对应的一个排列.
的最大值,并指出所对应的一个排列.
(Ⅲ)当 时,在一个排列中交换相邻两数的位置称为一次调整,若要求每次调整时波动强度不增加,问对任意排列
时,在一个排列中交换相邻两数的位置称为一次调整,若要求每次调整时波动强度不增加,问对任意排列 ,是否一定可以经过有限次调整使其波动强度降为9;若可以,给出调整方案,若不可以,请给出一个反例并加以说明.
,是否一定可以经过有限次调整使其波动强度降为9;若可以,给出调整方案,若不可以,请给出一个反例并加以说明.
(本小题满分14分)已知椭圆 :
: 的上顶点为
的上顶点为 ,两个焦点为
,两个焦点为 、
、 ,
, 为正三角形且周长为6.
为正三角形且周长为6.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)已知圆 :
: ,若直线
,若直线 与椭圆
与椭圆 只有一个公共点
只有一个公共点 ,且直线
,且直线 与圆
与圆 相切于点
相切于点 ;求
;求 的最大值.
的最大值.
(本小题满分13分)函数 ,其中
,其中 为常数,且
为常数,且 .
.
(Ⅰ)若曲线 在点(1,
在点(1, )处的切线与直线
)处的切线与直线 垂直,求
垂直,求 的值;
的值;
(Ⅱ)若函数 在区间[1,2]上的最小值为
在区间[1,2]上的最小值为 ,求
,求 的值.
的值.
(本小题满分14分)某中学在高二开设了A,B,C,D共4门选修课,每个学生必须且只需选修1门选修课,对于该年级的甲、乙、丙3名学生。
(Ⅰ)求这3名学生选择的选修课互不相同的概率;
(Ⅱ)求恰有2门选修课没有被这3名学生选择的概率;
(Ⅲ)求A选修课被这3名学生选择的人数的数学期望.
如图,在四棱锥P—ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABC是边长为2的菱形,∠BAD=60°,M为PC的中点.
(Ⅰ)求证:PA//平面BDM;
(Ⅱ)在AD上确定一点 ,使得面
,使得面 面
面 ,并加以证明;
,并加以证明;
(Ⅲ)求直线AC与平面ADM所成角的正弦值.