张聪与李明为得到一张去上海看世博会的门票,各自设计了一种方案。
张聪:如图是一个可以自由转动的转盘,随意转动转盘,当指针指向阴影区域时,张聪得到门票,否则李明得到门票。
李明:将三个完全相同的小球分别标上数字1,2,3后,放入一个不透明袋子中,从中随机取出一个小球,然后放回袋子混合均匀后,再随机取出一个小球,若两次取出的小球上数字之和为偶数,李明得到门票,否则张聪得到门票。
请你运用所学概率的知识,分析张聪和李明的设计方案对双方是否公平。
某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:1.第三组的频数是12.请你回答: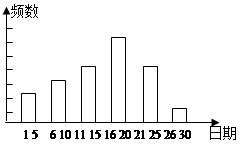
(1)本次活动共有件作品参赛;
(2)若将各组所占百分比绘制成扇形统计图,那么第四组对应的扇形的圆心角是度。
(3)本次活动共评出2个一等奖和3个二等奖及三等奖、优秀奖若干名,对一、二等奖作品进行编号并制作成背面完全一致的卡片,背面朝上的放置,随机抽出两张卡片,抽到的作品恰好一个是一等奖,一个是二等奖的概率是多少?
如图,点A、B、C分别是⊙O上的点,CD是⊙O的直径,P是CD延长线上的一点,AP=AC.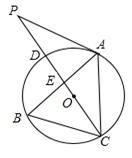
(1)若∠ABC=60°.求证:AP是⊙O的切线;
(2)若点B是弧CD的中点,AB交CD于点E,CD=4,求BE•AB的值.
如图(1),在直角坐标系xOy中,抛物线与x轴交于A、B两点,交y轴于点C,过A点的直线与抛物线的另一交点为D(m,3),与y轴相交于点E,点A的坐标为(-1,0),∠BAD=45°,点P是抛物线上的一点,且点P在第一象限.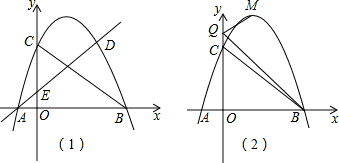
(1)求直线AD和抛物线的解析式;
(2)若S△PBC:S△BOC=2:3,求点P的坐标;
(3)如图(2),若M为抛物线的顶点,点Q为y轴上一点,求使QM+QB最小时,点Q的坐标,并求QM+QB的最小值.
如图,在等腰直角三角形ABC和DEC中,∠BCA=∠DCE=90°,点E在边AB上,ED与AC交于点F,连接AD.
(1)求证:△BCE≌△ACD.
(2)求证:AB⊥AD.
某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)满足一次函数且关系如下表:
| 时间t(天) |
1 |
3 |
6 |
10 |
36 |
… |
| 日销售量m(件) |
94 |
90 |
84 |
76 |
24 |
… |
未来40天内,每天的销售价格y(元)与时间t(天)的函数关系式如下:
| 每天的销售价格y(元) |
当1≤t≤20时,y1= t+25 t+25 |
当20<t≤40时,y2= t+40 t+40 |
(1)求日销售量m(件)与时间t(天)的函数关系;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少;
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元(a<4)给希望工程,公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.