某地举办乒乓球比赛的费用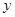 (元)包括两部分:一部分是租用比赛场地等固定不变的费用
(元)包括两部分:一部分是租用比赛场地等固定不变的费用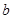 (元),另一部分费用与参加比赛的人数
(元),另一部分费用与参加比赛的人数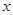 (人)成正比。当
(人)成正比。当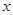 =20时,
=20时,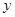 =1600;当
=1600;当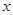 =30时,
=30时,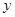 =2000;
=2000;
1)求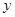 与
与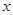 之间的函数关系式
之间的函数关系式
2)如果承办此次比赛的组委会共筹集到经费6250元,那么这次比赛最多可邀请多少名运动员参赛?
如图,四边形 是正方形, 、 分别是 、 上的一点,且 ,垂足为 ,求证: .
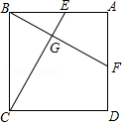
如图,抛物线 的图象与 轴交于 、 两点,与 轴交于 点,已知 点坐标为 .
(1)求抛物线的解析式;
(2)试探究 的外接圆的圆心位置,并求出圆心坐标;
(3)若点 是线段 下方的抛物线上一点,求 的面积的最大值,并求出此时 点的坐标.
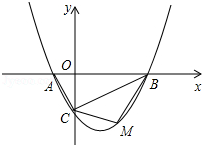
如图, 和 是有公共顶点的等腰直角三角形, ,点 为射线 , 的交点.
(1)求证: ;
(2)若 , ,把 绕点 旋转,当 时,求 的长;

某商品的进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为 元 为正整数),每个月的销售利润为 元.
(1)当每件商品的售价是多少元时,每个月的利润刚好是2250元?
(2)当每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
如图,在 中, ,点 在 上,以 为半径的 交 于点 , 的垂直平分线交 于点 ,交 于点 ,连接 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , , ,求线段 的长.
