以下茎叶图记录了甲,乙两个组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树为19的概率。
甲 组 乙 组
9 9 0 X 8 9
1 1 1 0
(本小题满分16分)已知数列 中,
中,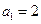 ,
, ,其前
,其前 项和
项和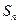 满足
满足 其中(
其中( ,
, ).
).
(1)求数列 的通项公式;
的通项公式;
(2)设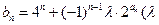 为非零整数,
为非零整数, ),试确定
),试确定 的值,使得对任意
的值,使得对任意 ,都有
,都有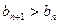 成立.
成立.
(本小题满分16分) 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数 以及D中的任意两数
以及D中的任意两数 ,恒有
,恒有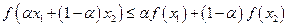 ,则称
,则称 为定义在D上的C函数.
为定义在D上的C函数.
(Ⅰ)试判断函数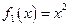 ,
, 中哪些是各自定义域上的C函数,并说明理由;
中哪些是各自定义域上的C函数,并说明理由;
(Ⅱ)已知 是R上的C函数,m是给定的正整数,设
是R上的C函数,m是给定的正整数,设 ,且
,且 ,记
,记 . 对于满足条件的任意函数
. 对于满足条件的任意函数 ,试求
,试求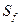 的最大值;
的最大值;
本小题满分15分)将数列 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:




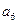




……
记表中的第一列数 构成的数列为
构成的数列为 ,
, .
. 为数列
为数列 的前
的前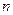 项和,且满足
项和,且满足 .
.
(Ⅰ)证明数列 成等差数列,并求数列
成等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当 时,求上表中第
时,求上表中第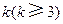 行所有项的和.
行所有项的和.
已知圆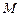 :
: ,设点
,设点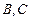 是直线
是直线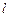 :
: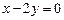 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点
,点 在线段
在线段 上,过
上,过 点作圆
点作圆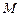 的切线
的切线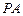 ,切点为
,切点为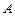 .
.
(1)若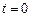 ,
, ,求直线
,求直线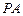 的方程;
的方程;
(2)经过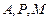 三点的圆的圆心是
三点的圆的圆心是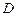 ,求线段
,求线段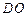 长的最小值
长的最小值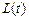 .
.
.设集合 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列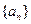 的集合:
的集合:
① ②
②
 是与
是与 无关的常数.
无关的常数.
(Ⅰ)若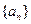 是等差数列,
是等差数列,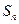 是其前n项的和,
是其前n项的和,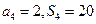 ,证明:
,证明: ;
;
(Ⅱ)设数列 的通项为
的通项为 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设数列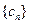 的各项均为正整数,且
的各项均为正整数,且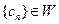 ,试证
,试证 .
.