在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相同数字的概率;
(Ⅱ)求取出的两个球上标号之积能被3整除的概率.
设有两个命题,p:关于x的不等式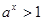 (a>0,且a≠1)的解集是{x|x<0};q:函数
(a>0,且a≠1)的解集是{x|x<0};q:函数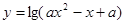 的定义域为R。如果
的定义域为R。如果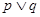 为真命题,
为真命题, 为假命题,求实数a的取值范围。
为假命题,求实数a的取值范围。
向量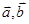 满足
满足 ,
, .
.
(1)求 关于k的解析式
关于k的解析式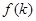 ;
;
(2)请你分别探讨 ⊥
⊥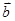 和
和 ∥
∥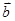 的可能性,若不可能,请说明理由,若可能,求出k的值;
的可能性,若不可能,请说明理由,若可能,求出k的值;
求 与
与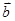 夹角的最大值.
夹角的最大值.
函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
(1)求实数 的值.(2)用定义证明
的值.(2)用定义证明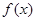 在
在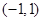 上是增函数;
上是增函数;
(3)写出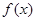 的单调减区间,并判断
的单调减区间,并判断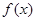 有无最大值或最小值?如有,写出最大值或最小值(无需说明理由)
有无最大值或最小值?如有,写出最大值或最小值(无需说明理由)
已知函数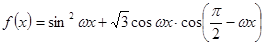 ,
,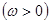 且函数
且函数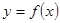 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为
(Ⅰ)求 的值;
的值; (Ⅱ)若函数
(Ⅱ)若函数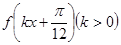 在区间
在区间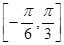 上单调递增,求k的取值范围.
上单调递增,求k的取值范围.