如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;
(3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
一个三棱柱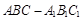 的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设 为线段
为线段 上的点.
上的点.
(1)求几何体 的体积;
的体积;
(2)是否存在点E,使平面 平面
平面 ,若存在,求AE的长.
,若存在,求AE的长.
已知等差数列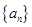 满足:
满足: ,
, ,
,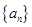 的前n项和为
的前n项和为 .
.
(1)求 及
及 ;
;
(2)令bn= (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.
已知向量 ,函数
,函数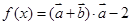 .
.
(1)求函数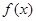 的最小正周期
的最小正周期 ;
;
(2)已知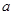 、
、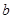 、
、 分别为
分别为 内角
内角 、
、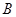 、
、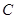 的对边, 其中
的对边, 其中 为锐角,
为锐角, ,且
,且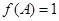 ,求
,求 和
和 的面积
的面积 .
.
如图,在底面为平行四边形的四棱锥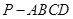 中,
中, 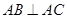 ,
,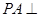 平面
平面 ,点
,点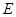 是
是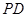 的中点.
的中点.
(1)求证: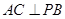 ;
;
(2)求证: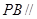 平面
平面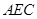 ;
;
已知函数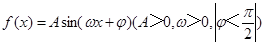 的图象在y轴上的截距为1,它在y轴右侧的第一个最高点和最低点分别为
的图象在y轴上的截距为1,它在y轴右侧的第一个最高点和最低点分别为 和
和
(1)求函数 的解析式;
的解析式;
(2)求函数f(x)的最小正周期和单调增区间.
(3)函数 的图像由
的图像由 怎样变换来的
怎样变换来的
(4)若 ,求函数y=f(x)的最大值和最小值以及取最值时对应的x的值
,求函数y=f(x)的最大值和最小值以及取最值时对应的x的值