定义在R上的函数f(x)是最小正周期为2的奇函数, 且当x∈(0, 1)时, f (x)=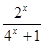 .
.
(1)求f (x)在[-1, 1]上的解析式;
(2)证明f (x)在(—1, 0)上时减函数;
(3)当λ取何值时, 不等式f (x)>λ在R上有解?
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点.
(1)求证:DE∥平面PFB;
(2)已知二面角P-BF-C的余弦值为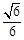 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积. 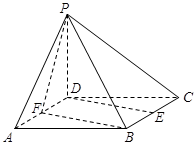
已知函数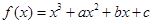 ,曲线
,曲线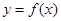 在点
在点 处的切线为
处的切线为 ,若
,若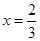 时,
时,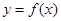 有极值.
有极值.
(1)求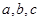 的值;
的值;
(2)求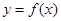 在
在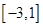 上的最大值和最小值.
上的最大值和最小值.
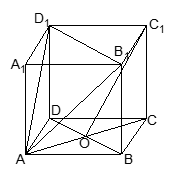
已知正方体ABCD-A1B1C1D1,
O是底面ABCD对角线的交点.
(1)求证:A1C⊥平面AB1D1;
(2)求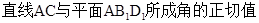 .
.
已知函数 在
在 与
与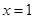 时都取得极值.
时都取得极值.
(1)求 的值及函数
的值及函数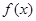 的单调区间;
的单调区间;
(2)若对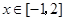 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图,直线 与抛物线
与抛物线 交于
交于 两点,与
两点,与 轴相交于点
轴相交于点 ,且
,且 .
.
(1)求证: 点的坐标为
点的坐标为 ;
;
(2)求证: ;
;
(3)求 的面积的最小值.
的面积的最小值.