如图,在一条笔直的高速公路MN的同旁有两上城镇A、B,它们与MN的距离分别是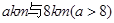 ,A、B在MN上的射影P、Q之间距离为12km,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为50万元/km;而每个与高速公路连接的立交出入口修建费用为200万元。设计部门提交了以下三种修路方案:
,A、B在MN上的射影P、Q之间距离为12km,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为50万元/km;而每个与高速公路连接的立交出入口修建费用为200万元。设计部门提交了以下三种修路方案:
方案①:两城镇各修一条普通公路到高速公路,并各修一个立交出入口;
方案②:两城镇各修一条普通公路到高速公路上某一点K,并在K点修一个公共立交出入口;
方案③:从A修一条普通公路到B,现从B修一条普通公路到高速公路,也只修一个立交出入口。
请你为这两个城镇选择一个省钱的修路方案。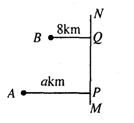
已知圆 ,直线
,直线 ,以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
,以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
(1)将圆C和直线 方程化为极坐标方程;
方程化为极坐标方程;
(2)P是 上的点,射线OP交圆C于点R,又点Q在OP上且满足
上的点,射线OP交圆C于点R,又点Q在OP上且满足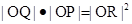 ,当点P在
,当点P在 上移动时,求点Q轨迹的极坐标方程.
上移动时,求点Q轨迹的极坐标方程.
如图,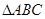 内接于
内接于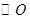 上,
上,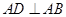 ,
,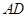 交
交 于点E,点F在DA的延长线上,
于点E,点F在DA的延长线上,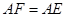 ,求证:
,求证: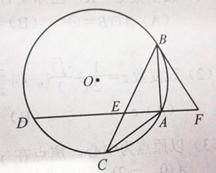
(1) 是
是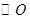 的切线;
的切线;
(2)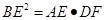 .
.
已知函数 .
.
(1)证明: ;
;
(2)当 时,
时, ,求
,求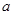 的取值范围.
的取值范围.
已知抛物线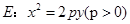 ,直线
,直线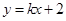 与E交于A、B两点,且
与E交于A、B两点,且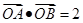 ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为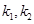 ,证明:
,证明: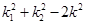 为定值.
为定值.
据民生所望,相关部门对所属服务单位进行整治行核查,规定:从甲类3个指标项中随机抽取2项,从乙类2个指标项中随机抽取1项.在所抽查的3个指标项中,3项都优秀的奖励10万元;只有甲类2项优秀的奖励6万元;甲类只有1项优秀、乙类1项优秀的提出警告,有2项或2项以上不优秀的停业运营并罚款8万元.已知某家服务单位甲类3项指标项中有2项优秀,乙类2项指标项中有1项优秀.
求:(1)这家单位受到奖励的概率;
(2)这家单位这次整治性核查中所获金额的均值(奖励为正数,罚款为负数).