如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a、b的值。
解:(1)A:____,D:_____B:____,
E:____,C:____,F:_____
特征:________________________________
(2)
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm.如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
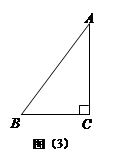
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)
问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:四边形DBFE的面积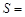 ,△EFC的面积
,△EFC的面积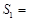 ,△ADE的面积
,△ADE的面积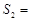 .
.
探究发现
(2)在(1)中,若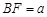 ,
,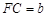 ,DE与BC间的距离为
,DE与BC间的距离为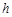 .请证明
.请证明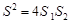 .
.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.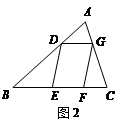
年春季,我国云南、贵州等西南地区遇到多年不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农及田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩.
(1)设甲种柴油发电机数量为x台,乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的函数关系式;
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元,应如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用W最少?
如图1,抛物线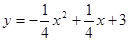 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线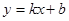 交于A、D两点。
交于A、D两点。
⑴直接写出A、C两点坐标和直线AD的解析式;
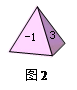
⑵如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点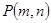 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?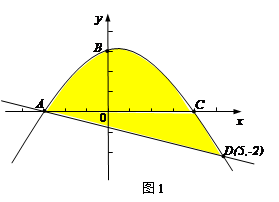
在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.