在图所示的平面直角坐标系中表示下面各点:。
A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7)。
(1)A点到原点O的距离是__ __个单位长。
(2)将点C向左平移6个单位,它会与点 重合。
(3)连接CE,则直线CE与 轴是什么位置关系?
轴是什么位置关系?
(4)点F到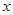 、
、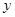 轴的距离分别是多少?
轴的距离分别是多少?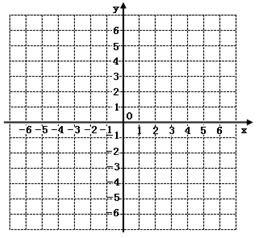
如图,点A、B、C、D在同一条直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.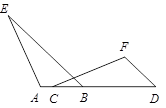
在平面直角坐标系xOy中,对于点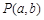 和点
和点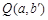 ,给出如下定义:若
,给出如下定义:若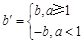 ,则称点
,则称点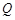 为点
为点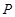 的限变点.例如:点
的限变点.例如:点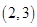 的限变点的坐标是
的限变点的坐标是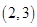 ,点
,点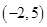 的限变点的坐标是
的限变点的坐标是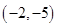 .
.
(1)①点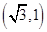 的限变点的坐标是___________;
的限变点的坐标是___________;
②在点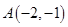 ,
,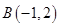 中有一个点是函数
中有一个点是函数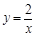 图象上某一个点的限变点,这个点是_______________;
图象上某一个点的限变点,这个点是_______________;
(2)若点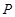 在函数
在函数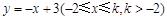 的图象上,其限变点
的图象上,其限变点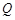 的纵坐标
的纵坐标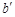 的取值范围是
的取值范围是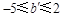 ,求
,求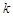 的取值范围;
的取值范围;
(3)若点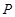 在关于
在关于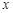 的二次函数
的二次函数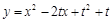 的图象上,其限变点
的图象上,其限变点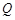 的纵坐标
的纵坐标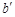 的取值范围是
的取值范围是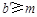 或
或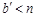 ,其中
,其中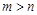 .令
.令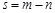 ,求
,求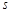 关于
关于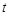 的函数解析式及
的函数解析式及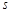 的取值范围.
的取值范围.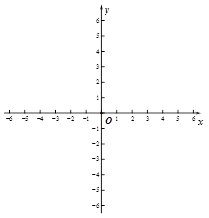
在菱形 中,
中,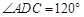 ,点
,点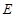 是对角线
是对角线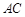 上一点,连接
上一点,连接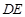 ,
,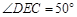 ,将线段
,将线段 绕点
绕点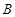 逆时针旋转
逆时针旋转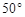 并延长得到射线
并延长得到射线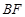 ,交
,交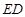 的延长线于点
的延长线于点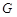 .
.
(1)依题意补全图形;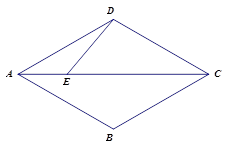
(2)求证: ;
;
(3)用等式表示线段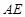 ,
,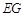 ,
,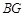 之间的数量关系:_____________________________.
之间的数量关系:_____________________________.
在平面直角坐标系xOy中,抛物线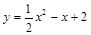 与
与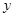 轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.
轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.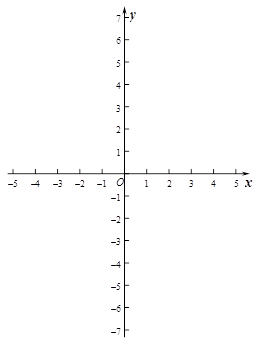
(1)求直线BC的解析式;
(2)点D在抛物线上,且点D的横坐标为4.将抛物线在点A,D之间的部分(包含点A,D)记为图象G,若图象G向下平移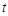 (
( )个单位后与直线BC只有一个公共点,求
)个单位后与直线BC只有一个公共点,求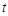 的取值范围.
的取值范围.
阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).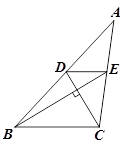
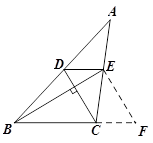
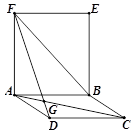
图1图2图3
请回答:BC+DE的值为_______.
参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.