(本题满分l0分)已知在平面直角坐标系中,点A,点B的坐标分别为A(0,0),B(0,4)点C在x轴上,且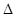 ABC的面积为6,求点C的坐标。
ABC的面积为6,求点C的坐标。
中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.
(注 参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为 度;
条形统计图中,喜欢“豆沙”月饼的学生有 人;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”月饼的共有 人.
(3)甲同学最爱吃云腿月饼,乙同学最爱吃豆沙月饼,现有重量、包装完全一样的云腿、豆沙、莲蓉、蛋黄四种月饼各一个,让甲、乙每人各选一个,请用画树状图法或列表法,求出甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率.
如图,在平面直角坐标系中,直角 的三个顶点分别是 , ,
(1)将 以点 为旋转中心旋转 ,画出旋转后对应的△ ;
(2)分别连接 、 后,求四边形 的面积.

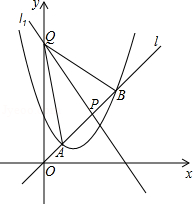
已知抛物线 ,直线 ,当 时,抛物线 与直线 只有一个公共点.
(1)求 的值;
(2)若直线 与抛物线 交于不同的两点 , ,直线 与直线 交于点 ,且 ,求 的值;
(3)在(2)的条件下,设直线 与 轴交于点 ,问:是否在实数 使 ?若存在,求 的值,若不存在,说明理由.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为 米.
(1)若苗圃园的面积为72平方米,求 ;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出 的取值范围.

问题引入:
(1)如图①,在 中,点 是 和 平分线的交点,若 ,则 (用 表示);如图②, , , ,则 (用 表示)
拓展研究:
(2)如图③, , , ,请猜想 (用 表示),并说明理由.
类比研究:
(3) 、 分别是 的外角 、 的 等分线,它们交于点 , , , ,请猜想 .
