经过调查发现，某一时尚产品在投放市场的30天中,前20天其价格呈直线上升，后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示：
| 时间 |
第4天 |
第12天 |
第21天 |
第28天 |
| 价格(百元) |
34 |
42 |
48 |
34 |
（1）写出价格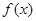
关于时间
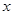的函数表达式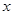（表示投放市场的第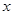天）；
（2）若销售量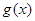
与时间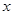的函数关系式为：
，
问该产品投放市场第几天，日销售额最高?
已知函数
(1)若函数
的图象与x轴无交点，求a的取值范围；
(2) 若函数在[-1,1]上存在零点，求a的取值范围；
(3)设函数
，当
时，若对任意的
，总存在
，使得
，求b的取值范围.
某地区为了了解某地区高中生的身体发育情况，对某一中学的随机抽取的50名学生的体重进行了测量，结果如下：（单位：kg）
42,38,29,36,41,43,54,43,34,44,40,59,39,42,44,50,37,44,45,29,48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,,67,53，49,65,47,54,63,58,43,46,58.
| 分组 |
频数 |
频率 |
频率/组距 |
| [27,32) |
0.06 |
||
| [32,37) |
0.06 |
||
| [37,42) |
9 |
||
| [42,47) |
0.064 |
||
| [47,52) |
7 |
||
| [52,57) |
5 |
||
| [57,62) |
4 |
||
| [62,67) |
0.06 |
（1）若以组距为5，完成下面样本频率分布表：
（2）根据（1）中的频率分布表，画出频率分布直方图；
（3）若本地区学生总人数为3000人，试根据抽样比例，估计本地区学生体重在区间[37,57]内所占的人数约为多少人？
某研究机构对高三学生的记忆力x和判断力y进行统计分析，得下表数据：
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
（1）请在图中画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（3）试根据（2）求出的线性回归方程，预测记忆力为9的同学的判断力.
某市电视台在因特网上征集电视节目的现场参与观众，报名的共有12000人，分别来自4个城区，其中东城区2400人，西城区4600人，南城区3800人，北城区1200人，从中抽取60人参加现场节目，应当如何抽取？
已知定义在R上的函数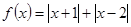
的最小值为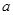
．
（1）求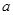的值；
（2）若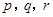
为正实数，且
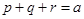，求证：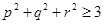
．