如图,隧道的截面由抛物线 和矩形
和矩形 构成,矩形的长
构成,矩形的长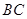 为
为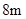 ,宽
,宽 为
为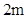 ,以
,以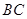 所在的直线为
所在的直线为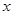 轴,线段
轴,线段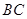 的中垂线为
的中垂线为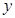 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,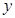 轴是抛物线的对称轴,顶点
轴是抛物线的对称轴,顶点 到坐标原点
到坐标原点 的距离为
的距离为 .
.
(1)求抛物线的解析式; (2)一辆货运卡车高
(2)一辆货运卡车高 ,宽2.4m,它能通过该隧道吗?
,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双行道,为了安全起见,在隧道正中间设
有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
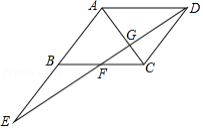
如图,在平行四边形 中,连接对角线 ,延长 至点 ,使 ,连接 ,分别交 , 交于点 , .
(1)求证: ;
(2)若 , ,求 的长.
先化简,再求值: ,然后从0,1,2三个数中选择一个恰当的数代入求值.
计算: .
如图1, 的三个顶点 、 、 分别落在抛物线 的图象上,点 的横坐标为 ,点 的纵坐标为 .(点 在点 的左侧)
(1)求点 、 的坐标;
(2)将 绕点 逆时针旋转 得到△ ,抛物线 经过 、 两点,已知点 为抛物线 的对称轴上一定点,且点 恰好在以 为直径的圆上,连接 、 ,求△ 的面积;
(3)如图2,延长 交抛物线 于点 ,连接 ,在坐标轴上是否存在点 ,使得以 、 、 为顶点的三角形与△ 相似.若存在,请求出点 的坐标;若不存在,请说明理由.

操作体验:如图,在矩形 中,点 、 分别在边 、 上,将矩形 沿直线 折叠,使点 恰好与点 重合,点 落在点 处.点 为直线 上一动点(不与 、 重合),过点 分别作直线 、 的垂线,垂足分别为点 和 ,以 、 为邻边构造平行四边形 .
(1)如图1,求证: ;
(2)特例感知:如图2,若 , ,当点 在线段 上运动时,求平行四边形 的周长;
(3)类比探究:若 , .
①如图3,当点 在线段 的延长线上运动时,试用含 、 的式子表示 与 之间的数量关系,并证明;
②如图4,当点 在线段 的延长线上运动时,请直接用含 、 的式子表示 与 之间的数量关系.(不要求写证明过程)
