(本小题满分6分)某风景区内有一古塔AB,在塔的北面有一建筑物,当光线与水平面的夹角是30°时,塔在建筑物的墙上留下了高3米的影子CD;而当光线与地面的夹角是45°时,塔尖A在地面上的影子E与墙角C有15米的距离(B、E、C在一条直线上),求塔AB的高度(结果保留根号). 
中国“最美扶贫高铁”之一的“张吉怀高铁”开通后,张家界到怀化的运行时间由原来的 小时缩短至 小时,运行里程缩短了 千米.已知高铁的平均速度比普通列车的平均速度每小时快 千米,求高铁的平均速度.

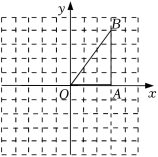
如图所示的方格纸( 格长为一个单位长度)中, 的顶点坐标分别为 .
(1)将 沿 轴向左平移 个单位,画出平移后的 (不写作法,但要标出顶点字母);
(2)将 绕点 顺时针旋转 ,画出旋转后的 (不写作法,但要标出顶点字母);
(3)在(2)的条件下,求点 绕点 旋转到点 所经过的路径长(结果保留 ).
先化简 ,再从 中选一个适当的数代入求值.
计算: .
综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平;
操作二:在 上选一点 ,沿 折叠,使点 落在矩形内部点 处,把纸片展平,连接 .
根据以上操作,当点 在 上时,写出图1中一个 的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片 按照(1)中的方式操作,并延长 交 于点 ,连接 .
①如图2,当点 在 上时, ______ , ______ ;
②改变点 在 上的位置(点 不与点 重合),如图3,判断 与 的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片 的边长为 ,当 时,直接写出 的长.
