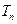已知函数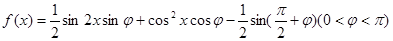 ,其图象过点
,其图象过点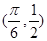 .
.
(1)求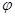 的值;
的值;
(2)将函数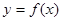 的图象上各点的横坐标缩短为原来的
的图象上各点的横坐标缩短为原来的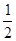 ,纵坐标不变,得到函数
,纵坐标不变,得到函数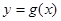 的图象,求函数
的图象,求函数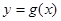 在区间
在区间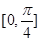 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)已知点 ,过点
,过点 作抛物线
作抛物线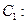
 的切线
的切线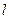 ,切点
,切点 在第二象限,如图.
在第二象限,如图.
(Ⅰ)求切点 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为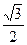 的椭圆
的椭圆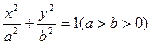 恰好经过切点
恰好经过切点 ,设切线
,设切线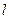 交椭圆的另一点为
交椭圆的另一点为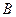 ,记切线
,记切线 的斜率分别为
的斜率分别为 ,若
,若 ,求椭圆方程.
,求椭圆方程.
(本小题满分12分)自然状态下的鱼类是一种可再生的资源,为了持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响。用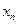 表示某鱼群在第
表示某鱼群在第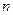 年初的总量,
年初的总量,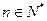 ,且
,且 。不考虑其他因素,设在第
。不考虑其他因素,设在第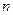 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与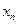 成正比,死亡量与
成正比,死亡量与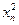 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数 其中
其中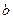 称为捕捞强度。
称为捕捞强度。
(1)求 与
与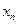 的关系式;
的关系式;
(2)设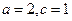 ,为了保证对任
,为了保证对任 意
意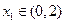 ,都有
,都有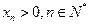 ,则捕捞强度
,则捕捞强度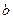 的最大允许值是多少?证明你的结论。
的最大允许值是多少?证明你的结论。
(本小题满分12分)已知函数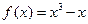 ,其图像记为
,其图像记为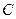 ,若对于任意非零实数
,若对于任意非零实数 ,曲线
,曲线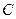 与其在点
与其在点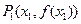 处的切线交于另一点
处的切线交于另一点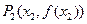 ,曲线
,曲线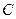 与其在点
与其在点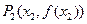 处的切线交于另一点
处的切线交于另一点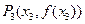 ,线段
,线段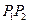 ,
,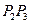 与曲线
与曲线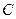 所围成封闭图形的面积分别记为
所围成封闭图形的面积分别记为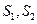 ,求证:
,求证: 为定值;
为定值;
(本小题满分12分)(1)对于定义在 上的函数
上的函数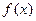 ,满足
,满足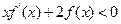 ,求证:函数
,求证:函数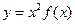 在
在 上是减函数;
上是减函数;
(2)请你认真研读(1)中命题并联系以下命题:若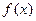 是定义在
是定义在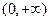 上的可导函数,满足
上的可导函数,满足 ,则
,则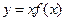 是
是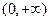 上的减函数。然后填空建立一个普遍化的命题
上的减函数。然后填空建立一个普遍化的命题 :
:
设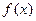 是定义在
是定义在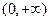 上的可导函数,
上的可导函数, ,若
,若 +
+
 ,
,
则是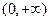 上的减函数。
上的减函数。
注:命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合;或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
(3)证明(2)中建立的普遍化命题。
(本小题共13分)设数列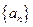 的前
的前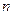 项和
项和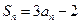
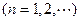 .
.
(Ⅰ)证明数列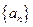 是等比数列;
是等比数列;
(Ⅱ)若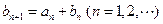
 ,且
,且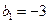 ,求数列
,求数列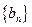 的前
的前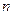 项和
项和