已知函数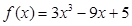
.
（Ⅰ）求函数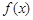
的单调递增区间；
（Ⅱ）求函数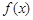在
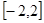的最大值和最小值.
某人上午7：00乘汽车以v1千米/小时（30≤v1≤100）匀速从A地出发到距300公里的B地，在B地不作停留，然后骑摩托车以v2千米/小时（4≤v2≤20）匀速从B地出发到距50公里的C地，计划在当天16：00至21：00到达C地．设乘汽车、骑摩托车的时间分别是x，y小时，如果已知所需的经费P=100+3（5﹣x）+2（8﹣y）元，那么v1，v2分别是多少时走的最经济，此时花费多少元？
已知向量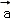
=（
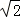cosωx，1），
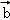=（2sin（ωx+
），﹣1）（其中
≤ω≤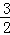
），
函数f（x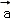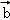）=•，且f（x）图象的一条对称轴为x=
．
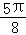（1）求f（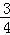
π）的值；
（2）若f（
）=
，f（
﹣
）=
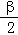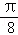，且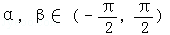
，
求cos（α﹣β）的值．
在△ABC中，角A，B，C的对应边分别是a，b，c满足b2+c2=bc+a2．
（Ⅰ）求角A的大小；
（Ⅱ）已知等差数列{an}的公差不为零，若a
cosA=1，且a 2 ，a 4 ，a 8成等比数列，求{
}的前n项和Sn．
如图，在四棱锥P﹣ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
（1）若PA=PD，求证：平面PQB⊥平面PAD；
（2）若平面PAD⊥平面ABCD，且PA=PD=AD=2，点M在线段PC上，且PM=3MC，求三棱锥P﹣QBM的体积．
已知数列{an}满足a1="3" ，
（
），数列{bn}满足
．
（1）证明数列{bn}是等差数列并求数列{bn}的通项公式；
（2）求数列{a n}的前n项和S n．