在△ABC中，角A，B，C的对应边分别是a，b，c满足b2+c2=bc+a2．
（Ⅰ）求角A的大小；
（Ⅱ）已知等差数列{an}的公差不为零，若a
cosA=1，且a 2 ，a 4 ，a 8成等比数列，求{
}的前n项和Sn．
（本小题满分12分）已知函数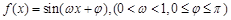
是R上的偶函数，其图象关于点M
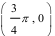对称
（1）求
的值；
（2）求
的单调递增区间；
（3）x∈
，求f（x）的最大值与最小值．
（本小题满分12分）已知2件次品和3件正品混放在一起，现需要通过检测将其区分，
每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测
结束．
（1）求第一次检测出的是次品且第二次检测出的是正品的概率；
（2）己知每检测一件产品需要费用1 00元，设X表示直到检测出2件次品或者检测
出3件正品时所需要的检测费用（单位：元），求X的分布列和均值（数学期望）．
（本小题满分10分）己知关于x的不等式|x+a|<b的解集为{x|2<x<4）
（1）求实数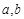
的值；
（2）求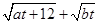
的最大值．
（本小题满分10分）在直角坐标系xOy中，曲线C1
（t为参数，t≠0），
其中0≤
<π，在以O为极点， x轴正半轴为极轴的极坐标系中，曲线
C2 : 
,C3 : 
（1）求C2与C3交点的直角坐标；
（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．
（本小题满分10分）选修4—5：不等式选讲
已知
．
（1）关于
的不等式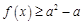
恒成立，求实数
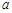的取值范围；
（2）设
，且
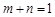，求证：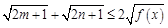
．