小莉的爸爸有一张电影门票，她和哥哥两人都想去观看，可门票只有一张，读九年级的哥哥想了个办法，拿出八张扑克牌，将数字1，2，3，5的四张给妹妹，将数字4，6，7，8的四张留给自己，并按下列游戏规则进行：小莉和哥哥从各自的牌中随机抽出一张，然后两张牌的数字相加，如果和为偶数，则小莉去，如果和为奇数则哥哥去．
（1）用树状图或列表法求小莉能去看电影的概率．
（2）哥哥设计的游戏规则公平吗？请说明理由。
已知一元二次方程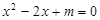
。
（1）若方程有两个实数根，求m的范围；
（2）若方程的两个实数根为x1，x2，且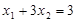
，求m的值。
如图，PA与⊙O相切于A点，弦AB⊥OP，垂足为C，OP与⊙O相交于D点，已知OA=2，OP=4。
（1）求∠POA的度数；
（2）计算弦AB的长。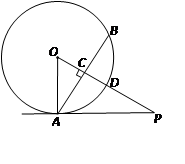
如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点
均在格点上，在建立平面直角坐标系后，点A的坐标为（－6，1），点B的坐标为（－3，1），
点C的坐标为（－3，3）。
（1）将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1的图形，并写出点A1的坐标；
（2）将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形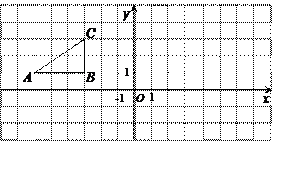
解方程组：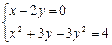
（本小题满分14分）已知二次函数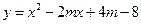
（1）当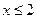
时，函数值
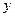随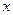
的增大而减小，求
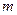的取值范围。
（2）以抛物线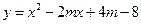的顶点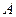
为一个顶点作该抛物线的内接正三角形
（
，
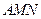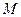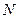两点在抛物线上），请问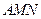：△的面积是与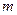无关的定值吗？若是，请求出这个定值；若不是，请说明理由。
（3）若抛物线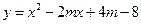与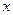轴交点的横坐标均为整数，求整数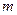的值。