(本小题满分10分)在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为
(0°＜＜180°)，得到△A1B1C．
(1)如图1，当AB∥CB1时，设A1B1与BC相交于点D．证明：△A1CD是等边三角形；
(2)如图2，连接AA1、BB1，设△ACA1和△BCB1的面积分别为S1、S2．
求证：S1∶S2＝1∶3；
(3)如图3，设AC的中点为E，A1B1的中点为P，AC＝a，连接EP．当等于多少度时，EP的长度最大，最大值是多少？
如图所示，已知四边形OABC是菱形，∠O=60°，点M是边OA的中点，以点O为圆心，r为半径作⊙O分别交OA，OC于点D，E，连接BM．若BM=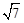
，
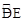的长是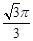
．求证：直线BC与⊙O相切．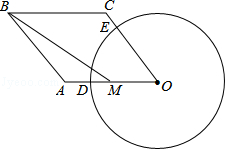
已知点O是平面直角坐标系的原点，直线y=﹣x+m+n与双曲线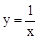
交于两个不同的点A（m，n）（m≥2）和B（p，q）．直线y=﹣x+m+n与y轴交于点C，求△OBC的面积S的取值范围．
如图所示，在正方形ABCD中，点G是边BC上任意一点，DE⊥AG，垂足为E，延长DE交AB于点F．在线段AG上取点H，使得AG=DE+HG，连接BH．求证：∠ABH=∠CDE．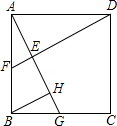
一个有进水管与出水管的容器，从某时刻开始的3分内只进水不出水，在随后的9分内既进水又出水，每分的进水量和出水量都是常数．容器内的水量y（单位：升）与时间x（单位：分）之间的关系如图所示．当容器内的水量大于5升时，求时间x的取值范围．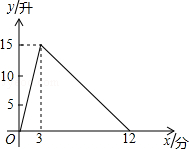
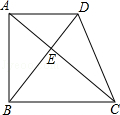
如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点E．若AE=4，CE=8，DE=3，梯形ABCD的高是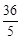
，面积是54．求证：AC⊥BD．