已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如下,且f(x)=ln x-h(x).
(1)求函数f(x)在x=1处的切线斜率;
(2)若函数f(x)在上是单调函数,求实数m的取值范围;
(3)若函数y=2x-lnx(x∈[1,4])的图象总在函数y=f(x)的图象的上方,求c的取值范围.
在直角坐标系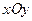 中,直线
中,直线 的参数方程为
的参数方程为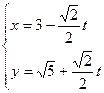 (
(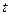 为参数),在极
为参数),在极
坐标系(与直角坐标系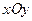 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,圆C的方程为
轴正半轴为极轴)中,圆C的方程为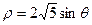 。
。
①求圆C的直角坐标方程;
②设圆C与直线 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为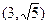 ,求|PA|+|PB|。
,求|PA|+|PB|。
(本题满分12分)下面的一组图形为某一四棱锥S-ABCD的侧面与底面。
(1)请画出四棱锥S-ABCD的直观图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA 面ABCD,E为AB中点,求二面角E-SC-D的大小;
面ABCD,E为AB中点,求二面角E-SC-D的大小;
(3)求点D到面S EC的距离。
EC的距离。
(本题满分10分)已知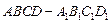 是底面为正方形的长方体,
是底面为正方形的长方体, ,
, ,点
,点 是
是 上的动点.
上的动点.
(1)求证:不论点 在
在 上的任何位置,平面
上的任何位置,平面 都垂直于平面
都垂直于平面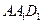
(2)当 为
为 的中点时,求异面直线
的中点时,求异面直线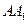 与
与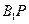 所成角的余弦值;
所成角的余弦值;
(本题满分10分)已知数列 为等差数列,
为等差数列, ,
, ,数列
,数列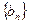 的前
的前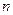 项和为
项和为 ,且有
,且有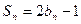
(1)求 、
、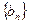 的通项公式;(2)若
的通项公式;(2)若 ,
, 的前
的前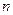 项和为
项和为 ,求
,求 .
.
(本题满分10分) 如图,在直三棱柱 中,
中,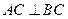 ,点
,点 是
是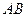 的中点.,求证:(1)
的中点.,求证:(1)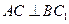 ;(2)
;(2) 平面
平面 .
.