已知10件不同产品中有4件是次品,现对它们进行一一测试,直到选出所有4件次品为止。
(1)若恰在第5次测试,才测试到第一件次品,第十次才找到最后一件次品的不同测试方法数是多少?
(2)若恰在第5次测试后,就找出了所有4件次品,则这样的不同测试方法数是多少?
已知 ;
;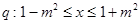 .
.
(Ⅰ)若 是
是 的必要条件,求
的必要条件,求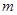 的取值范围;
的取值范围;
(Ⅱ)若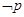 是
是 的必要不充分条件,求
的必要不充分条件,求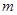 的取值范围.
的取值范围.
设关于x的不等式|2x﹣1|<t|x|.
(1)当t=2时,不等式|2x﹣1|<t|x|+a对∀x∈R恒成立,求实数a的取值范围;
(2)若原不等式的解中整数解恰有2个,求实数t的取值范围.
已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若曲线C1的方程为ρ2=8ρsinθ﹣15,曲线 C2的方程为 (
( 为参数).
为参数).
(1)将C1的方程化为直角坐标方程;
(2)若C2上的点Q对应的参数为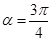 ,P为C1上的动点,求PQ的最小值.
,P为C1上的动点,求PQ的最小值.
如图所示,AB是半径为1的圆O的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.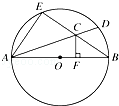
(1)求证:AE•BC=AC•BD;
(2)求BC•BE+AC•AD的值.
已知函数f(x)=1﹣ax+lnx,
(1)若函数在x=2处的切线斜率为 ,求实数a的值;
,求实数a的值;
(2)若存在x∈(0,+∞)使f(x)≥0成立,求实数a的范围;
(3)证明对于任意n∈N,n≥2有: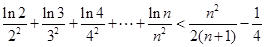 .
.