如图所示,AB是半径为1的圆O的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.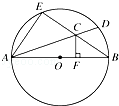
(1)求证:AE•BC=AC•BD;
(2)求BC•BE+AC•AD的值.
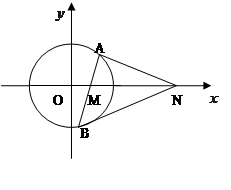
(本小题满分16分)如图,已知圆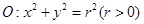 ,动直线
,动直线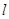 过点
过点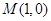 交圆
交圆 于
于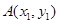 ,
, 两点(点
两点(点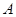 在
在 轴上方),点
轴上方),点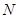 在
在 轴上,若点
轴上,若点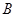 的坐标为
的坐标为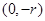 ,则点
,则点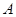 的横坐标为
的横坐标为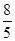 .
.
(1)求 的值;
的值;
(2)当直线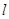 的斜率为
的斜率为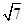 时,直线
时,直线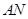 与圆
与圆 相切,求点
相切,求点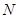 的坐标;
的坐标;
(3)试问:是否存在一定点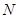 ,使得
,使得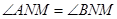 总成立?若存在,请求出点
总成立?若存在,请求出点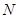 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分16分)如图,在平面直角坐标系 中,
中,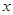 轴在地平面上,
轴在地平面上, 轴垂直于地面,
轴垂直于地面,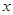 轴、
轴、 轴上的单位长度都为
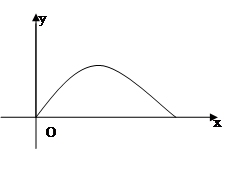
轴上的单位长度都为 ,某炮位于坐标原点处,炮弹发射后,其路径为抛物线
,某炮位于坐标原点处,炮弹发射后,其路径为抛物线 的一部分,其中
的一部分,其中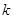 与炮弹的发射角有关且
与炮弹的发射角有关且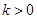 .
.
(1)当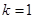 时,求炮弹的射程;
时,求炮弹的射程;
(2)对任意正数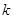 ,求炮弹能击中的飞行物的高度
,求炮弹能击中的飞行物的高度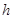 的取值范围;
的取值范围;
(3)设一飞行物(忽略大小)的高度为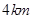 ,试求它的横坐标
,试求它的横坐标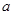 不超过多少
不超过多少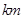 时,炮弹可以击中它.(答案精确到
时,炮弹可以击中它.(答案精确到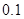 ,
, 取
取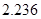 )
)
(本小题满分16分)在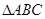 中,角
中,角 所对的边分别为
所对的边分别为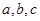 ,已知
,已知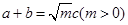 .
.
(1)当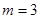 时,
时,
①若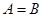 ,求
,求 ;
;
②若 ,求
,求 的值;
的值;
(2)当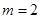 时,若
时,若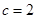 ,求
,求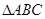 面积最大值.
面积最大值.
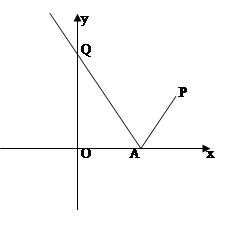
(本小题满分14分)如图,已知过点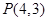 的光线,经
的光线,经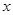 轴上一点
轴上一点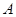 反射后的射线
反射后的射线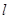 过点
过点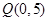 .
.
(1)求点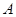 的坐标;
的坐标;
(2)若圆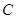 过点
过点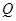 且与
且与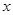 轴相切于点
轴相切于点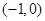 ,求圆
,求圆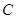 的方程.
的方程.
(本小题满分14分)如图,在正三棱柱 中,
中,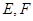 分别为
分别为 中点.
中点.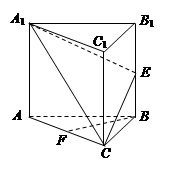
(1)求证: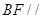 平面
平面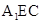 ;
;
(2)求证:平面 平面
平面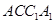 .
.