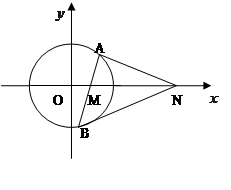
(本小题满分16分)如图,已知圆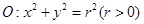 ,动直线
,动直线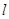 过点
过点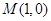 交圆
交圆 于
于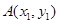 ,
, 两点(点
两点(点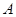 在
在 轴上方),点
轴上方),点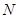 在
在 轴上,若点
轴上,若点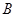 的坐标为
的坐标为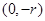 ,则点
,则点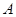 的横坐标为
的横坐标为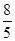 .
.
(1)求 的值;
的值;
(2)当直线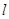 的斜率为
的斜率为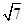 时,直线
时,直线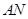 与圆
与圆 相切,求点
相切,求点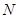 的坐标;
的坐标;
(3)试问:是否存在一定点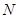 ,使得
,使得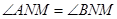 总成立?若存在,请求出点
总成立?若存在,请求出点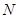 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知{an}的前n项和Sn,an>0且an2+2an=4Sn+3
(1)求{an}的通项公式;
(2)若bn=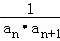 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.
(1)若a=1.5,问:观察者离墙多远时,视角θ最大?
(2)若tanθ=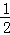 ,当a变化时,求x的取值范围.
,当a变化时,求x的取值范围.
已知
(1)若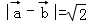 ,求证:
,求证: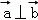
(2)设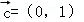 ,若
,若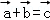 ,求α,β的值.
,求α,β的值.
如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点
(1)求证:PE⊥BC;
(2)求证:EF∥平面PAD.
在△ABC中,角A,B,C所对的边分别为a,b,c,且acosB=bcosA.
(1)求证:a=b
(2)若sinA= ,求sin(C
,求sin(C )的值.
)的值.