已知
求:
求矩阵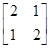 的特征值及对应的特征向量.
的特征值及对应的特征向量.
若点A(1,1)在矩阵M=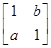 对应变换的作用下得到的点为B(-1,1),求矩阵M的逆矩阵.
对应变换的作用下得到的点为B(-1,1),求矩阵M的逆矩阵.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.
证明:
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
如图,已知圆上的弧 ,过C点的圆的切线与BA的延长线交于E点,
,过C点的圆的切线与BA的延长线交于E点,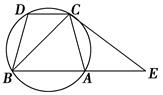
证明:
(1)∠ACE=∠BCD;
(2)BC2=BE·CD.