已知数列{an}满足:a1=1,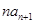 =2(n十1)an+n(n+1),(
=2(n十1)an+n(n+1),(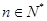 ),
),
(I)若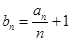 ,试证明数列{bn}为等比数列;
,试证明数列{bn}为等比数列;
(II)求数列{an}的通项公式an与前n项和Sn.
(本小题满分13分)
袋子中装有编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球.
(Ⅰ)写出所有不同的结果;
(Ⅱ)求恰好摸出1个黑球和1个红球的概率;
(Ⅲ) 求至少摸出1个黑球的概率.
(本小题满分13分)
在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
,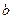 ,
, ,且
,且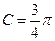 ,
,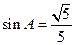 .
.
(Ⅰ)求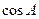 ,
,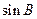 的值;
的值;
(Ⅱ)若 ,求
,求 ,
,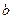 的值.
的值.
(本小题共13分)
已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(Ⅰ)求证:{ }是等差数列;
}是等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若 ,求证:
,求证:  .
.
(本小题共14分)
已知椭圆的中心在原点,焦点在 轴上,经过点
轴上,经过点
 且离心率
且离心率 .过定点
.过定点 的直线与椭圆相交于
的直线与椭圆相交于 ,
, 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)在 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存
的坐标;若不存
在,请说明理由.
(本小题共14分)
已知函数 在
在 与
与 处都取得极值.
处都取得极值.
(Ⅰ)求 的值及函数
的值及函数 的单调区间;
的单调区间;
(Ⅱ)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.