在直角梯形PBCD中A为PD的中点,如下左图。 ,将
,将 沿AB折到
沿AB折到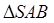 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下右图。
,如下右图。
(1)求证: 平面ABCD;(2)求二面角E—AC—D的正切值.
平面ABCD;(2)求二面角E—AC—D的正切值.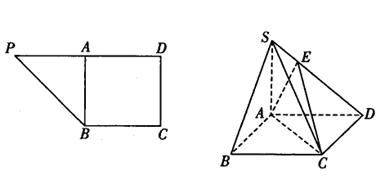
如图,四棱锥P-ABCD中,底面ABCD是正方形,O是正方形ABCD的中心,PO⊥底面ABCD,E是PC的中点,求证:
(1)PA∥平面BDE;
(2)平面PAC⊥平面BDE.
已知全集U=R,集合M={x|x≤a-2或x≥a+3},N={x|-1≤x≤2}.
(1)若 ,求(
,求( )∩(
)∩( );
);
(2)若 ∩
∩ =
= ,求实数
,求实数 的取值范围.
的取值范围.
已知函数 ,
, .
.
(Ⅰ)若函数 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅱ)设直线 为函数
为函数 的图象上一点
的图象上一点 处的切线.证明:在区间
处的切线.证明:在区间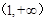 上存在唯一的
上存在唯一的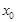 ,使得直线
,使得直线 与曲线
与曲线 相切.
相切.
等差数列 中,
中,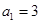 ,前
,前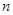 项和为
项和为 ,等比数列
,等比数列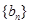 各项均为正数,
各项均为正数,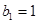 ,且
,且 ,
,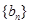 的公比
的公比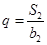
(1)求 与
与 ;
;
(2)证明:
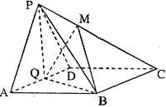
如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形,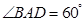 ,
,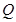 为
为 的中点。
的中点。
(1)若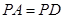 ,求证:平面
,求证:平面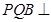 平面
平面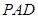 ;
;
(2)点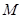 在线段
在线段 上,
上, ,试确定
,试确定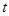 的值,使
的值,使 平面
平面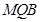 ;
; (3)在(2)的条件下,若平面
(3)在(2)的条件下,若平面 平面ABCD,且
平面ABCD,且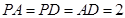 ,求二面角
,求二面角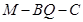 的大小。
的大小。