已知函数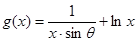 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且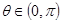 ,
, ,
, ∈R.
∈R.
(1)求θ的值;
(2)若 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设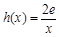 ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个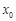 ,使得
,使得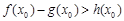 成立,求
成立,求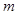 的取值范围.
的取值范围.
如图示,已知平行四边形ABCD和矩形ACEF所在平面互相垂直,AB=1,AD=2, 是线段EF的中点.
是线段EF的中点.
(1)求证: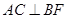 ;
;
(2)设二面角A—FD—B的大小为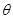 ,求
,求 的值;
的值;
(3)设点P为一动点,若点P从M出发,沿棱按照 的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.
的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.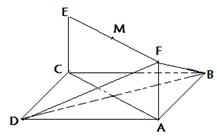
在数列 中,已知
中,已知 ,且
,且 .
.
(1)若数列 为等差数列,求p的值;
为等差数列,求p的值;
(2)求数列 的通项公式;
的通项公式;
某市某房地产公司售楼部,对最近100位采用分期付款的购房者进行统计,统计结果如下表所示:
| 付款方式 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频数 |
40 |
20 |
a |
10 |
b |
已知分3期付款的频率为0.2,售楼部销售一套某户型的住房,顾客分1期付款,其利润为10万元;分2期、3期付款其利润都为15万元;分4期、5期付款其利润都为20万元,用 表示销售一套该户型住房的利润。
表示销售一套该户型住房的利润。
(1)求上表中a,b的值;
(2)若以频率分为概率,求事件A:“购买该户型住房的3位顾客中,至多有1位采用分3期付款”的概率P(A);
(3)若以频率作为概率,求 的分布列及数学期望E
的分布列及数学期望E .
.
已知向量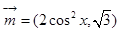 ,
, ,函数
,函数 ,
,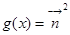 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)在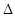
 中,
中,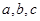 分别是角
分别是角 的对边,R为
的对边,R为 外接圆的半径,且
外接圆的半径,且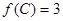 ,
,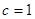 ,
, ,且
,且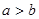 ,求
,求 的值.
的值.