某市某房地产公司售楼部，对最近100位采用分期付款的购房者进行统计，统计结果如下表所示：
| 付款方式 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频数 |
40 |
20 |
a |
10 |
b |
已知分3期付款的频率为0.2，售楼部销售一套某户型的住房，顾客分1期付款，其利润为10万元；分2期、3期付款其利润都为15万元；分4期、5期付款其利润都为20万元，用
表示销售一套该户型住房的利润。
（1）求上表中a,b的值；
（2）若以频率分为概率，求事件A：“购买该户型住房的3位顾客中，至多有1位采用分3期付款”的概率P（A）；
（3）若以频率作为概率，求的分布列及数学期望E.
(本小题满分12分)
已知数列{an}的前三项与数列{bn}的前三项对应相等，且a1＋2a2＋22a3＋…＋2n－1an＝8n对任意的n∈N*都成立，数列{bn＋1－bn}是等差数列.
(1)求数列{an}与{bn}的通项公式；
(2)是否存在k∈N*，使得bk－ak∈(0,1)？请说明理由.
(本小题满分12分)
已知函数f(x)＝2sinωx·cos(ωx＋)＋(ω>0)的最小正周期为4π.
(1)求正实数ω的值；
(2)在△ABC中，内角A、B、C的对边分别为a、b、c，且满足2bcosA＝acosC＋ccosA，求f(A)的值.
(本小题满分12分)
若盒中装有同一型号的灯泡共12只，其中有9只合格品，3只次品.
(1)某工人师傅有放回地连续从该盒中取灯泡3次，每次取一只灯泡，求2次取到次品的概率；
(2)某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡，每次从中取一灯泡，若是正品则用它更换已坏灯泡，若是次品则将其报废(不再放回原盒中)，求成功更换会议室的已坏灯泡前取出的次品灯泡只数X的分布列和数学期望.
选修4－5：不等式选讲
已知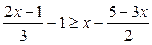
,求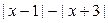 
的最大值和最小值.
选修4—4：坐标系与参数方程
已知直线的极坐标方程为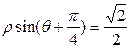
，圆M的参数方程为
。
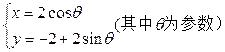（1）将直线的极坐标方程化为直角坐标方程；
（2）求圆M上的点到直线的距离的最小值.