(本小题满分12分)
已知数列{an}的前三项与数列{bn}的前三项对应相等,且a1+2a2+22a3+…+2n-1an=8n对任意的n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得bk-ak∈(0,1)?请说明理由.
(本小题满分12分)某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知该厂生产这种仪器,次品率p与日产量x(件)之间大体满足关系: .已知每生产一件合格的仪器可盈利A元,但每生产一件次品将亏损
.已知每生产一件合格的仪器可盈利A元,但每生产一件次品将亏损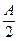 元,厂方希望定出适当的日产量.
元,厂方希望定出适当的日产量.
(1)试判断:当日产量(件)超过94件时,生产这种仪器能否赢利?并说明理由;
(2)当日产量x件不超过94件时,试将生产这种仪器每天的赢利额T(元)表示成日产量x(件)的函数;
(3)为了获得最大利润,日产量x件应为多少件?
(本小题满分12分)在△OAB中,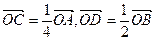 ,AD与BC交于点M,设
,AD与BC交于点M,设 =a,
=a, =b,
=b,
(1)用a,b表示 ;
;
(2)在线段AC上取一点E,在线段BD上取一点F,使EF过M点,设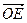 =p
=p ,
, =q
=q ,求证:
,求证: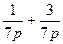 =1.
=1.
(本小题满分12分)如图,已知:PD⊥平面ABCD,AD⊥DC,AD∥BC,PD∶DC∶BC=1∶1∶ .
.
(1)求PB与平面PDC所成角的大小;
(2)求二面角D—PB—C的正切值.
(本小题满分12分)已知等差数列{an}的首项a1=1,公差d>0,且其第二项、第五项、第十四项分别是等比数列{bn}的第二、三、四项.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意自然数n均有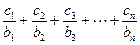 =an+1成立,求c1+c2+c3+…+c2003的值.
=an+1成立,求c1+c2+c3+…+c2003的值.
(本小题满分14分)椭圆E中心在原点O,焦点在x轴上,其离心率e=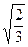 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段 的比为2.
的比为2.
(1)用直线l的斜率k(k≠0)表示△OAB的面积;
(2)当△OAB的面积最大时,求椭圆E的方程.