已知函数 ,
, .
.
(Ⅰ)若函数 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅱ)设直线 为函数
为函数 的图象上一点
的图象上一点 处的切线.证明:在区间
处的切线.证明:在区间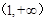 上存在唯一的
上存在唯一的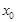 ,使得直线
,使得直线 与曲线
与曲线 相切.
相切.
(本小题满分12分)已知函数 ,
, .
.
(1)若 为曲线
为曲线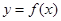 的一条切线,求a的值;
的一条切线,求a的值;
(2)若对任意的实数x都有 ,求a的取值范围.
,求a的取值范围.
(本小题满分12分)已知F是抛物线C: 的焦点,点
的焦点,点 在抛物线C上,且
在抛物线C上,且 ·
·
(1)求p,t的值;
(2)设O为坐标原点,抛物线C上是否存在点A(不考虑点A为C的顶点),使得过点O作线段OA的垂线与抛物线C交于点B,直线AB交x轴、y轴于点D、E, 表示△OAB的面积,
表示△OAB的面积, 表示△ODE的面积,满足
表示△ODE的面积,满足 ?若存在,求点A的坐标;若不存在,说明理由.
?若存在,求点A的坐标;若不存在,说明理由.
(本小题满分12分)如图,多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB//cD,AD⊥CD,AB=2,CD=4,直线BE与平面ABCD所成的角的正切值等于 .
.
(1)求证:平面BCE⊥平面BDE;
(2)求多面体体ABCDEF的体积.
(本小题满分12分)为了了解中学生的体能状况,某校抽取了n名高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中第二小组频数为7.
(1)求频率分布直方图中a的值及抽取的学生人数n;
(2)现从跳绳次数在[179.5,199.5]内的学生中随机选取2人,求至少有一人跳绳次数在[189.5,199.5]之间的概率。
(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,已知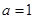 ,A=
,A= ,
,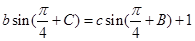 .
.
(1)求B,C的值;
(2)求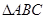 的面积.
的面积.