已知 为坐标原点,
为坐标原点, ,
, (
( ,
, 是常数),若
是常数),若
(1)求 关于
关于 的函数关系式
的函数关系式 ;
;
(2)若 的最大值为
的最大值为 ,求
,求 的值;
的值;
(3)利用(2)的结论,用“五点法”作出函数 在长度为一个周期的闭区间上的简图,并指出其单调区间。
在长度为一个周期的闭区间上的简图,并指出其单调区间。
(理科)已知椭圆 经过点
经过点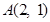 ,离心率为
,离心率为 .过点
.过点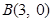 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 .
.
(Ⅰ)求椭圆 的方程;(Ⅱ)求
的方程;(Ⅱ)求 的取值范围;
的取值范围;
(Ⅲ)设直线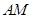 和直线
和直线 的斜率分别为
的斜率分别为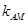 和
和 ,求证:
,求证: 为定值.
为定值.
(理科)已知椭圆C: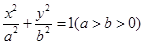 的离心率为
的离心率为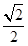 ,且经过点
,且经过点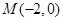 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l: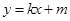 与椭圆C相交于
与椭圆C相交于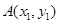 ,
, 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且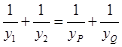 .求证:直线
.求证:直线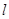 过定点.
过定点.
(理科)已知椭圆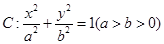 的两个焦点分别为
的两个焦点分别为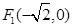 ,
,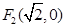 .点
.点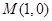 与椭圆短轴的两个端点的连线相互垂直.
与椭圆短轴的两个端点的连线相互垂直.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知点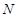 的坐标为
的坐标为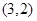 ,点
,点 的坐标为
的坐标为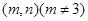 .过点
.过点 任作直线
任作直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,设直线
两点,设直线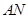 ,
,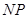 ,
,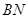 的斜率分别为
的斜率分别为 ,
,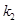 ,
,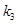 ,若
,若 ,试求
,试求 满足的关系式.
满足的关系式.
(理科)已知椭圆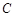 :
: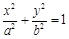 (
(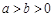 )的离心率
)的离心率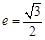 ,原点到过点
,原点到过点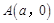 ,
,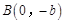 的直线的距离是
的直线的距离是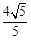 .
.
(1)求椭圆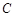 的方程;
的方程;
(2)若椭圆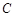 上一动点
上一动点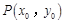 关于直线
关于直线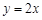 的对称点为
的对称点为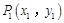 ,求
,求 的取值范围.
的取值范围.
(3)如果直线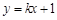 (
(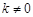 )交椭圆
)交椭圆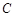 于不同的两点
于不同的两点 ,
, ,且
,且 ,
, 都在以
都在以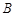 为圆心的圆上,求
为圆心的圆上,求 的值.
的值.
(理科)已知中心在原点,焦点在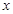 轴上的椭圆
轴上的椭圆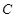 过点
过点 ,离心率为
,离心率为 ,点
,点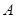 为其右顶点.过点
为其右顶点.过点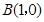 作直线
作直线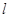 与椭圆
与椭圆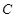 相交于
相交于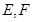 两点,直线
两点,直线 ,
,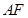 与直线
与直线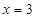 分别交于点
分别交于点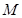 ,
, .
.
(Ⅰ)求椭圆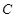 的方程;
的方程;
(Ⅱ)求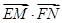 的取值范围.
的取值范围.