袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用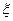 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(Ⅰ)取出的3个小球上的数字互不相同的概率;
(Ⅱ)随机变量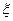 的概率分布和数学期望;
的概率分布和数学期望;
(Ⅲ)计分介于20分到40分之间的概率.
在 中,角
中,角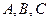 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
,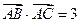 .
.
(Ⅰ)求 的面积;
的面积;
(Ⅱ)若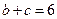 ,求
,求 的值.
的值.
已知动圆P过点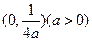 且与直线
且与直线 相切.
相切.
(Ⅰ) 求动圆圆心P的轨迹E的方程;
(Ⅱ) 设直线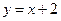 与轨迹E交于点A、B,M是线段AB的中点,过M作
与轨迹E交于点A、B,M是线段AB的中点,过M作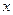 轴的垂线交轨迹E于N.
轴的垂线交轨迹E于N.
① 证明:轨迹E点N处的切线 与AB平行;
与AB平行;
② 是否存在实数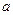 ,使
,使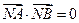 ?若存在,求
?若存在,求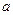 的值;若不存在,说明理由.
的值;若不存在,说明理由.
设函数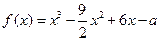 .
.
(Ⅰ) 对于任意实数 ,求证:
,求证: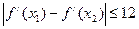 ;
;
(Ⅱ) 若方程 有且仅有一个实根,求
有且仅有一个实根,求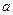 的取值范围.
的取值范围.
已知数列 满足:
满足:
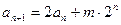
 (
( 是与无关的常数且
是与无关的常数且 ).
).
(Ⅰ) 设 ,证明数列
,证明数列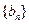 是等差数列,并求
是等差数列,并求 ;
;
(Ⅱ) 若数列 是单调递减数列,求
是单调递减数列,求 的取值范围.
的取值范围.