在数列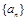 中,
中,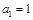 ,且对任意的
,且对任意的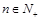 ,都有
,都有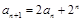 .
.
(1)求证:数列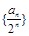 是等差数列;
是等差数列;
(2)设数列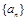 的前
的前 项和为
项和为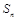 ,求证:对任意的
,求证:对任意的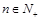 ,
,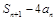 都为定值.
都为定值.
已知命题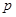 :方程
:方程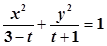 所表示的曲线为焦点在x轴上的椭圆;命题
所表示的曲线为焦点在x轴上的椭圆;命题 :实数
:实数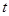 满足不等式
满足不等式 <0.
<0.
(1)若命题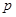 为真,求实数
为真,求实数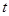 的取值范围;
的取值范围;
(2)若命题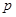 是命题
是命题 的充分不必要条件,求实数
的充分不必要条件,求实数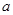 的取值范围
的取值范围
(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=lg .
.
(1)当m=5时,求函数f(x)的定义域;
(2)若关于x的不等式f(x)≥1的解集为R,求m的取值范围。
(本小题满分10分)选修4-4:坐标系与参数方程
在极坐标系中,已知圆 与直线
与直线 为参数)相切,求实数
为参数)相切,求实数 的值。
的值。
(本小题满分10分)选修4—1;几何证明选讲
如图,在△ABC 中, 以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE, AE交⊙O于点F
以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE, AE交⊙O于点F
(Ⅰ) 求证: 是⊙O的切线;
是⊙O的切线;
(Ⅱ) 若⊙O的直径为2,求 的值.
的值.
(本小题满分12分)已知 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行.
(1)求a,b满足的关系式;
(2)若 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;